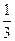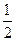题目内容
设向量
=(m,1),
=(2,-3),若满足
∥
,则m=( )
| a |
| b |
| a |
| b |
A.
| B.-
| C.
| D.-
|
∵
∥
,(
≠
),
∴存在唯一实数λ使得
=λ
,
∵
=(m,1),
=(2,-3),
∴(m,1)=λ(2,-3)=(2λ,-3λ),
即
=
,
解得:m=-
.
故选:D.
| a |
| b |
| b |
| 0 |
∴存在唯一实数λ使得
| a |
| b |
∵
| a |
| b |
∴(m,1)=λ(2,-3)=(2λ,-3λ),
即
| m |
| 2 |
| 1 |
| -3 |
解得:m=-
| 2 |
| 3 |
故选:D.

练习册系列答案
相关题目
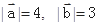 .(1)若
.(1)若 的夹角为60o,求
的夹角为60o,求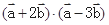 ;
;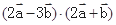 =61,求
=61,求 中,设
中,设 是
是 边上的一点,且满足
边上的一点,且满足 ,
, ,则
,则 的值为( )
的值为( )




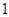


 ,
, 共线的充要条件是( )
共线的充要条件是( ) ,
,
 ,
,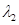 ,
,
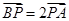 且
且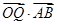 =1,则点P的轨迹方程是( )
=1,则点P的轨迹方程是( )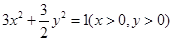
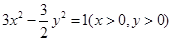
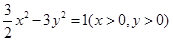
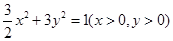
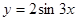 变为曲线
变为曲线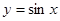 的伸缩变换是( )
的伸缩变换是( )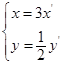
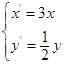
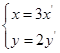
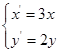
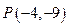 、
、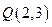 且
且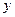 轴与线段
轴与线段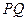 的交点为
的交点为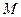 ,则点
,则点 所成的比为 ( )
所成的比为 ( )