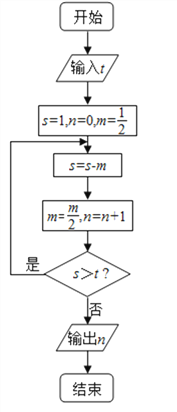
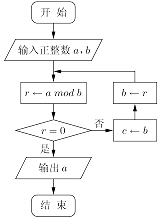
题目内容
【题目】如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2. 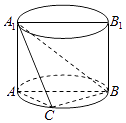
(1)求证:平面AA1C⊥平面BA1C;
(2)若AC=BC,求几何体A1﹣ABC的体积V.
【答案】
(1)证明:因为C是底面圆周上异于A,B的一点,AB是底面圆的直径,
所以AC⊥BC.
因为AA1⊥平面ABC,BC平面ABC,所以AA1⊥BC,
而AC∩AA1=A,所以BC⊥平面AA1C.
又BC平面BA1C,所以平面AA1C⊥平面BA1C
(2)解:在Rt△ABC中,AB=2,则由AB2=AC2+BC2且AC=BC,
得 ![]() ,
,
所以 ![]()
【解析】(1)证明BC⊥平面AA1C,即可证明平面AA1C⊥平面BA1C;(2)求出AC,直接利用体积公式求解即可.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目