题目内容
已知F1为椭圆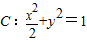
的左焦点，直线l：y=x-1与椭圆C交于A、B两点，那么|F1A|+|F1B|的值为 ．
【答案】分析：由椭圆方程求出F1点的坐标，联立方程组求出A、B两点，然后利用两点间断距离公式求出|F1A|+|F1B|的值．
解答：解：把y=x-1代入椭圆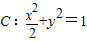
，并整理，得3x2-4x=0，
解得x1=0，y1=-1，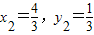
，
∴
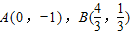，F1（-1，0），
∴|F1A|+|F1B|=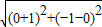
+
=
．
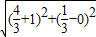
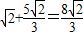故答案为：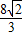
．
点评：本题考查直线和椭圆的位置关系，解题时要认真审题，仔细挖掘题设中的隐含条件．
解答：解：把y=x-1代入椭圆
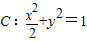，并整理，得3x2-4x=0，解得x1=0，y1=-1，
，∴
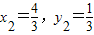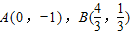，F1（-1，0），∴|F1A|+|F1B|=
+=
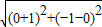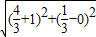
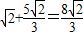．故答案为：
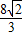．点评：本题考查直线和椭圆的位置关系，解题时要认真审题，仔细挖掘题设中的隐含条件．
练习册系列答案
相关题目
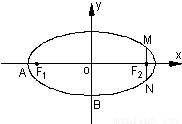
如图，在直角坐标系xOy中，已知椭圆C：
的离心率e＝
，左右两个焦分别为F1、F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|＝1．
，(
)试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上.
+
=1（a＞b＞0）的离心率e=
，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的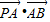
=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．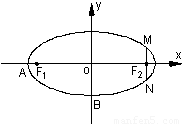
+
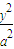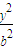=1（a＞b＞0）的离心率e=
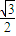，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的
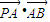=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．