题目内容
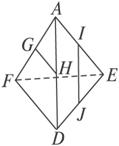
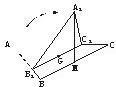 如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于B1、C1.将△AB1C1沿B1C1折起到△A1B1C1的位置,使点A1在平面BB1C1C上的射影恰是线段BC的中点M.求:
如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于B1、C1.将△AB1C1沿B1C1折起到△A1B1C1的位置,使点A1在平面BB1C1C上的射影恰是线段BC的中点M.求:(1)二面角A1-B1C1-M的大小;
(2)异面直线A1B1与CC1所成角的大小.(用反三角函数表示)
分析:(1)连接AM、A1G,根据二面角平面角的定义可知∠A1GM是二面角A1-B1C1-M的平面角,在Rt△A1GM中求出此角即可;
(2)B1作C1C的平行线交BC于点P,则∠A1B1P等于异面直线A1B1与CC1所成的角,在△A1B1P中利用余弦定理可求得∠A1B1P的大小.
(2)B1作C1C的平行线交BC于点P,则∠A1B1P等于异面直线A1B1与CC1所成的角,在△A1B1P中利用余弦定理可求得∠A1B1P的大小.
解答:解:(1)连接AM、A1G.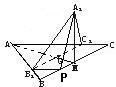
∵G是正三角形ABC的中心,且M为BC的中点,
∴A、G、M三点共线,AM⊥BC.
∵B1C1∥BC,∴B1C1⊥AM于点G,
即GM⊥B1C1,GA1⊥B1C1.
∴∠A1GM是二面角A1-B1C1-M的平面角.
∵点A1在平面BB1C1C上的射影为M,
∴A1M⊥MG,∠A1MG=90°.
在Rt△A1GM中,由A1G=AG=2GM,得∠A1GM=60°,
即二面角A1-B1C1-M的大小是60°.
(2)过B1作C1C的平行线交BC于点P,
则∠A1B1P等于异面直线A1B1与CC1所成的角.
由PB1C1C是平行四边形得B1P=C1C=1=BP,
PM=BM-BP=
,A1B1=AB1=2.
∵A1M⊥面BB1C1C于点M,
∴A1M⊥BC,∠A1MP=90°.
在Rt△A1GM中,A1M=A1G•sin60°=
•
=
.
在Rt△A1MP中,A1P2=A1M2+PM2=(
)2+(
)2=
.
在△A1B1P中,由余弦定理得
cos∠A1B1P=
=
=
,
∴异面直线A1B1与CC1所成角的大小为arccos
.

∵G是正三角形ABC的中心,且M为BC的中点,
∴A、G、M三点共线,AM⊥BC.
∵B1C1∥BC,∴B1C1⊥AM于点G,
即GM⊥B1C1,GA1⊥B1C1.
∴∠A1GM是二面角A1-B1C1-M的平面角.
∵点A1在平面BB1C1C上的射影为M,
∴A1M⊥MG,∠A1MG=90°.
在Rt△A1GM中,由A1G=AG=2GM,得∠A1GM=60°,
即二面角A1-B1C1-M的大小是60°.
(2)过B1作C1C的平行线交BC于点P,
则∠A1B1P等于异面直线A1B1与CC1所成的角.
由PB1C1C是平行四边形得B1P=C1C=1=BP,
PM=BM-BP=
| 1 |
| 2 |
∵A1M⊥面BB1C1C于点M,
∴A1M⊥BC,∠A1MP=90°.
在Rt△A1GM中,A1M=A1G•sin60°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
在Rt△A1MP中,A1P2=A1M2+PM2=(
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
在△A1B1P中,由余弦定理得
cos∠A1B1P=
| A1B12+B1P2-A1P2 |
| 2•A1B1•B1P |
22+12-
| ||
| 2•2•1 |
| 5 |
| 8 |
∴异面直线A1B1与CC1所成角的大小为arccos
| 5 |
| 8 |
点评:本小题主要考查异面直线所成的角,以及二面角等基础知识,考查空间想象能力,运算能力和推理论证能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目

 (λ>O,λ为变量)
(λ>O,λ为变量)