题目内容
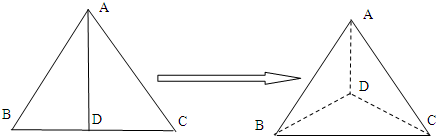
如图，正三角形ABC按中线AD折叠，使得二面角B-AD-C的大小为60°，则∠BAC的余弦值为
．
| 7 |
| 8 |
| 7 |
| 8 |
分析：根据正三角形ABC按中线AD折叠，二面角B-AD-C的大小为60°，可知，∠BDC=60°，从而在△ABC中，可求∠BAC的余弦值
解答：解：由题意，∠BDC=60°
假设正三角形的边长为2a，则BC=a
在△ABC中，AB=AC=2a
∴cos∠BAC=
=
故答案为
假设正三角形的边长为2a，则BC=a
在△ABC中，AB=AC=2a
∴cos∠BAC=
| 4a2+4a2-a2 |
| 2×2a×2a |
| 7 |
| 8 |
故答案为
| 7 |
| 8 |
点评：本题以正三角形为载体，主要考查平面图形的翻折问题，关键是搞清翻折前后变化与不变的量．
练习册系列答案
相关题目
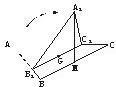如图，正三角形ABC的边长为3，过其中心G作BC边的平行线，分别交AB、AC于B1、C1．将△AB1C1沿B1C1折起到△A1B1C1的位置，使点A1在平面BB1C1C上的射影恰是线段BC的中点M．求：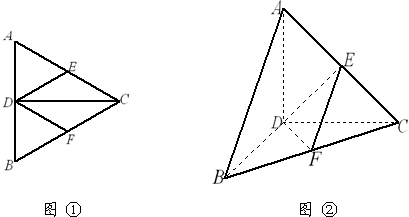
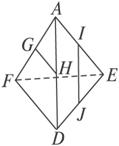
(λ＞O，λ为变量)