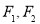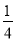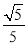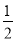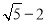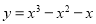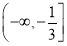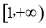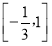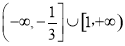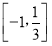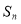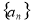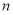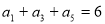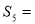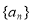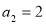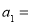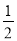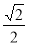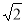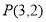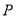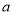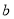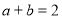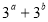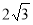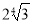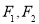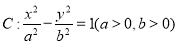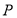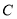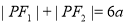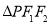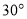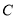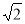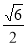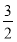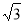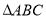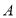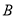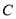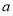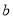题目内容
已知顶点是坐标原点,对称轴是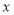 轴的抛物线经过点
轴的抛物线经过点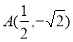 .
.
(1)求抛物线的标准方程;
(2)直线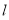 过定点
过定点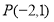 ,斜率为
,斜率为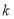 ,当
,当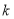 为何值时,直线与抛物线有公共点?
为何值时,直线与抛物线有公共点?
(1) 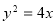 ;(2)
;(2) 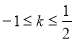 .
.
【解析】
试题分析:(1)顶点是坐标原点,对称轴是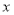 轴的抛物线经过第四象限点
轴的抛物线经过第四象限点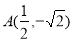 ,因此该抛物线开口向右,可设其标准方程为
,因此该抛物线开口向右,可设其标准方程为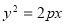 ,利用抛物线过点
,利用抛物线过点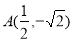 可求出
可求出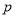 而得方程.
而得方程.
(2)点斜式写出直线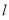 的方程
的方程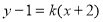 ,当方程组
,当方程组 有解时,直线与抛物线有公共点,故可在消去
有解时,直线与抛物线有公共点,故可在消去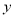 后利一元二次方程根的判别式求出
后利一元二次方程根的判别式求出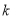 的取值范围.
的取值范围.
试题解析:【解析】
(1)依题意设抛物线的方程为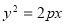 2分
2分
把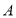 点的坐标
点的坐标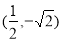 代入方程得
代入方程得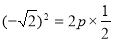
解得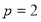 5分
5分
∴抛物线的标准方程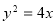 6分
6分
(2)直线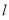 的方程为
的方程为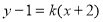 ,即
,即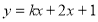 7分
7分
解联立方程组 ,消去
,消去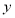 ,得
,得
得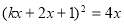 ,化简得
,化简得 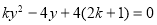 9分
9分
①当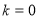 ,由①得
,由①得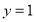 代入
代入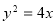 ,得
,得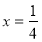
这时直线与抛物线有一个公共点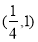 11分
11分
②当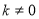 ,依题意得
,依题意得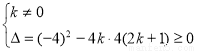
解得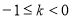 或
或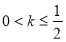 13分
13分
综合①②,当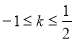 时直线与抛物线有公共点 14分
时直线与抛物线有公共点 14分
考点:1、抛物线的标准方程;2、直线与抛物线位置关系的判断;3、直线的方程.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目