题目内容
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知函数 .
.
(1) 试说明函数 的图像是由函数
的图像是由函数 的图像经过怎样的变换得到的;
的图像经过怎样的变换得到的;
(2) (理科)若函数 ,试判断函数
,试判断函数 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数 的最小正周期是
的最小正周期是 ;
;
(3) 求函数 的单调区间和值域.
的单调区间和值域.
【答案】
解(1)∵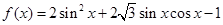
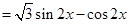 ,
,
∴ .
.
∴函数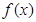 的图像可由
的图像可由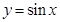 的图像按如下方式变换得到:
的图像按如下方式变换得到:
①将函数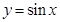 的图像向右平移
的图像向右平移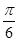 个单位,得到函数
个单位,得到函数 的图像;
的图像;
②将函数 的图像上所有点的横坐标缩短到原来的
的图像上所有点的横坐标缩短到原来的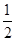 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数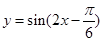 的图像;
的图像;
③将函数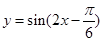 的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数 的图像.
的图像.
(2)(理科)由(1)知, ,
,
∴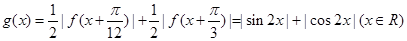 .
.
又对任意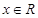 ,有
,有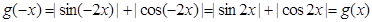 ,
,
∴函数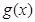 是偶函数.
是偶函数.
∵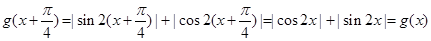 ,
,
∴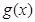 是周期函数,
是周期函数,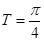 是它的一个周期.
是它的一个周期.
现用反证法证明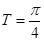 是函数
是函数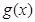 的最小正周期。
的最小正周期。
反证法:假设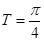 不是函数
不是函数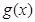 的最小正周期,设
的最小正周期,设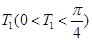 是
是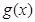 的最小正周期.
的最小正周期.
则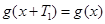 ,即
,即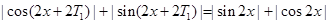 .
.
令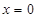 ,得
,得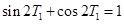 ,两边平方后化简,得
,两边平方后化简,得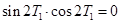 ,这与
,这与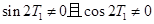 (
(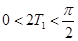 )矛盾.因此,假设不成立.
)矛盾.因此,假设不成立.
所以,函数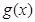 的最小正周期是
的最小正周期是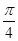 .
.
(3)(理科)先求函数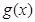 在一个周期
在一个周期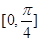 内的单调区间和函数值的取值范围。
内的单调区间和函数值的取值范围。
当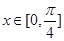 时,
时,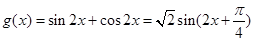 ,且
,且 .
.
易知,此时函数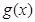 的单调增区间是
的单调增区间是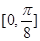 ,单调减区间是
,单调减区间是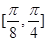 ;
;
函数的取值范围是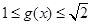 .
.
因此,依据周期函数的性质,可知函数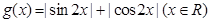 的单调增区间是
的单调增区间是
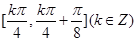 ;单调减区间是
;单调减区间是 ;
;
函数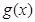 的值域是
的值域是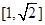 .
.
【解析】横坐标先放缩,再平移也可.即将函数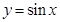 的图像上所有点的横坐标缩短到原来的
的图像上所有点的横坐标缩短到原来的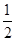 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数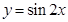 ,再将函数
,再将函数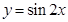 的图像向右平移
的图像向右平移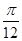 个单位,得到函数
个单位,得到函数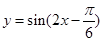 的图像,最后将函数
的图像,最后将函数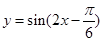 的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数 的图像.
的图像.

练习册系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处