题目内容
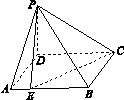
如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,当二面角P-EC-D的平面角为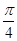 时,AE=( )
时,AE=( )
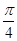 时,AE=( )
时,AE=( )
| A.1 | B. | C.2- | D.2- |
D
试题分析:以点D为原点,AD、DC、DP所在的直线为x、y、z轴,建立空间直角坐标系
则P(0,0,1),C(0,2,0),设E(1,y0,0),则
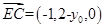 ,设平面PEC的法向量
,设平面PEC的法向量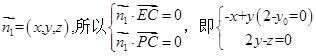 ,解得
,解得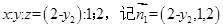 ,而平面ECD的法向量
,而平面ECD的法向量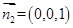 ,因为二面角P-EC-D的平面角为
,因为二面角P-EC-D的平面角为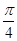 ,所以
,所以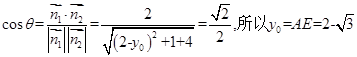 ,
,点评:此题重点考查了利用空间向量借助平面的法向量的夹角与二面角的大小之间的关系,同时还考查了利用方程的思想解出未知的变量.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 ,
, 是垂足.
是垂足.
 平面
平面 ;
;  ,求证:
,求证:

 .
.




 平面AEB,
平面AEB, ,
, ,
, ,
, ,
, ,
, ,G是BC的中点.
,G是BC的中点.
 ;
; 的大小.
的大小.


 ,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
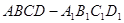 中.
中.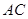 与
与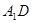 所成角的大小;
所成角的大小;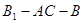 的正切值.
的正切值.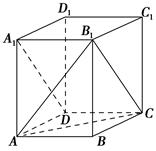
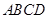 ,
,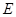 是
是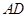 中点,则直线
中点,则直线 与直线
与直线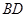 所成的角的余弦值为( )
所成的角的余弦值为( ) 


