题目内容
已知数列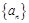 中,
中,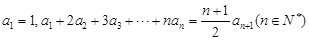
(Ⅰ)求数列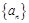 的通项
的通项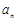 ;
;
(Ⅱ)求数列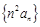 的前
的前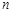 项和
项和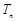 ;
;
(Ⅲ)若存在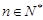 ,使得
,使得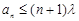 成立,求实数
成立,求实数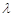 的最小值.
的最小值.
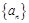 中,
中,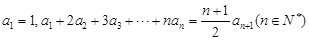
(Ⅰ)求数列
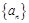 的通项
的通项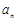 ;
;(Ⅱ)求数列
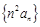 的前
的前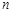 项和
项和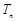 ;
;(Ⅲ)若存在
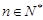 ,使得
,使得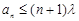 成立,求实数
成立,求实数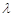 的最小值.
的最小值.(Ⅰ)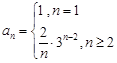 .
.
(Ⅱ)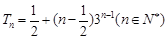 .
.
(Ⅲ)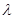 的最小值是
的最小值是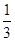 .
.
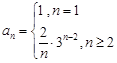 .
.(Ⅱ)
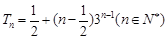 .
.(Ⅲ)
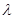 的最小值是
的最小值是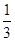 .
.试题分析:(Ⅰ)
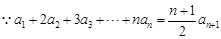 ,
,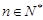 ①
①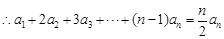 ,
,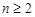 ②
②①-②:
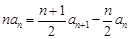 ,
,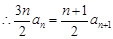 , 2分
, 2分即
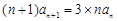 (
(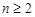 ),又
),又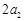 =2,
=2,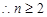 时,数列
时,数列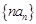 是以2为首项,3为公比的等比数列.
是以2为首项,3为公比的等比数列.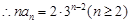 ,故
,故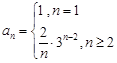 4分
4分(Ⅱ)由(Ⅰ)可知当
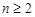 时,
时,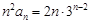 ,
,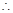 当
当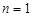 时,
时,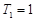 ;
;当
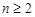 时,
时,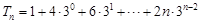 ,①
,①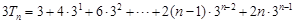 ,②
,②①-②得,
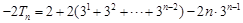
=
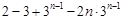
=
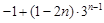
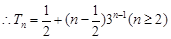 ,又
,又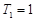 也满足
也满足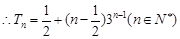 9分
9分(Ⅲ)
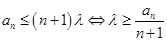 ,由(Ⅰ)可知:
,由(Ⅰ)可知:当
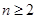 时,
时,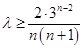 ,令
,令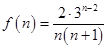 ,
,则
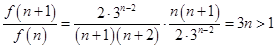 ,
,又
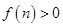 ,∴
,∴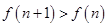
∴当
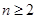 时,
时,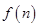 单增,∴
单增,∴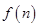 的最小值是
的最小值是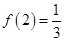
而
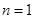 时,
时,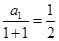 ,综上所述,
,综上所述,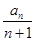 的最小值是
的最小值是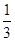
∴
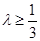 ,即
,即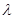 的最小值是
的最小值是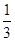 13分
13分点评:难题,为确定等差数列、等比数列的通项公式,往往通过建立相关元素的方程组,而达到目的。数列的求和问题,往往涉及“公式法”“分组求和法”“裂项相消法”“错位相减法”等。涉及不等式恒成立问题,通过放缩、求和等,得到最值。

练习册系列答案
相关题目
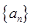 的首项
的首项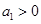 ,公比
,公比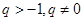 ,设数列
,设数列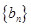 的通项公式
的通项公式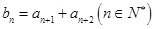 ,数列
,数列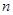 项和分别记为
项和分别记为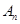 ,
,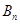 ,试比较
,试比较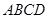 的面积为1,把它的各边延长一倍得到新正方形
的面积为1,把它的各边延长一倍得到新正方形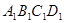 ,再把正方形
,再把正方形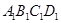 的各边延长一倍得到正方形
的各边延长一倍得到正方形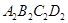 (如图2),如此进行下去,正方形
(如图2),如此进行下去,正方形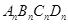 的面积为 .(用含有
的面积为 .(用含有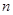 的式子表示,
的式子表示,
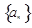 是等比数列,
是等比数列,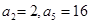 ,则公比
,则公比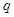 等于
等于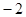
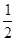
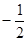
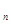 }的公比为正数,且a
}的公比为正数,且a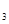 ·a
·a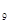 =2a
=2a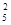 ,a
,a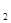 =1,则a
=1,则a =
=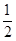
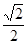
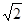
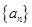 中,
中,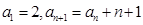 ,则通项
,则通项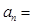 _ .
_ .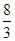 和
和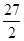 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .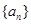 是首项为
是首项为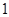 ,公比为
,公比为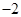 的等比数列,则
的等比数列,则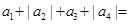 .
.