题目内容
已知等比数列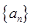 的首项
的首项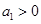 ,公比
,公比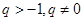 ,设数列
,设数列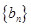 的通项公式
的通项公式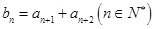 ,数列
,数列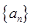 ,
,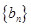 的前
的前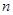 项和分别记为
项和分别记为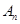 ,
,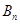 ,试比较
,试比较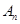 与
与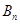 的大小.
的大小.
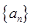 的首项
的首项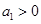 ,公比
,公比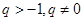 ,设数列
,设数列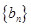 的通项公式
的通项公式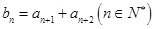 ,数列
,数列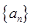 ,
,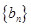 的前
的前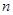 项和分别记为
项和分别记为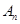 ,
,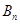 ,试比较
,试比较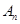 与
与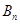 的大小.
的大小.当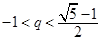 且
且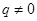 时,
时,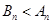 ;当
;当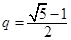 时,
时,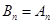 ;当
;当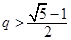 时,
时,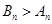 .
.
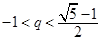 且
且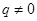 时,
时,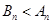 ;当
;当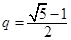 时,
时,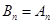 ;当
;当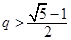 时,
时,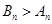 .
.试题分析:本题中,要讨论
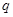 是否等于1.可以先将等比数列
是否等于1.可以先将等比数列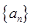 的前
的前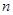 项和
项和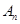 表示出来,再将
表示出来,再将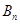 用
用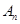 表示出来.以
表示出来.以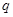 是否等于1分两大类讨论
是否等于1分两大类讨论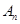 与
与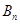 的大小.
的大小.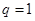 由
由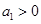 易知
易知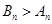 ;
;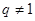 ,用作差法讨论
,用作差法讨论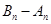 的正负以比较大小关系.注意将
的正负以比较大小关系.注意将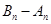 写成几个因式的乘积,通过判断各因式的正负来定
写成几个因式的乘积,通过判断各因式的正负来定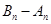 的正负.最后结合两大类讨论的情况作一总结.
的正负.最后结合两大类讨论的情况作一总结.试题解析:等比数列
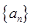 的首项
的首项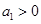 ,公比
,公比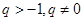 ,所以其前
,所以其前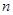 项和
项和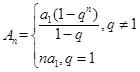 .
.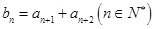 ,所以数列
,所以数列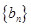 的前
的前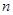 项和
项和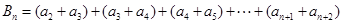
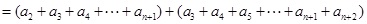

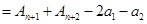
(1)当
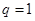 时,
时, ,
,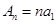 ,因为
,因为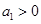 ,
,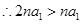 ,
,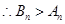 4分
4分(2)当
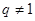 时,
时,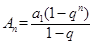 ,
,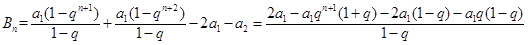
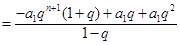
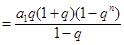 .
.所以
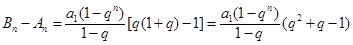 .令
.令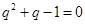 ,
,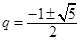 ,又因为
,又因为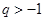 ,所以
,所以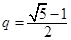 .因为
.因为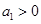 ,当
,当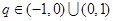 时,
时,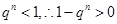 ,
,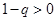 ,所以
,所以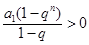 ,当
,当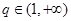 时,
时,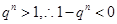 ,
,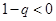 ,所以
,所以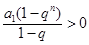 .故当
.故当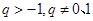 时,恒有
时,恒有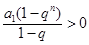
①当
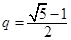 时,
时,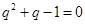 ,此时
,此时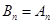 10分
10分②当
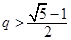 且
且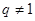 时,
时,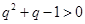 ,此时
,此时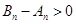 ,即
,即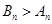 12分
12分③当
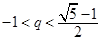 且
且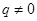 时,
时,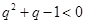 ,此时
,此时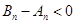 ,即
,即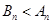 14分
14分综上所述,当
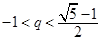 且
且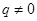 时,
时,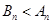 ;当
;当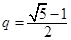 时,
时,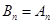 ;当
;当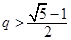 时,
时,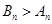 . 16分
. 16分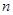 项和;2.作差法比较大小;3.一元二次不等式与相应的二次方程的联系.
项和;2.作差法比较大小;3.一元二次不等式与相应的二次方程的联系.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
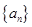 中,已知
中,已知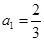 ,
,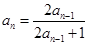 .
.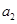 、
、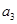 并判断
并判断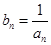 ,求证:
,求证: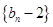 为等比数列;
为等比数列;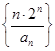 的前n项和
的前n项和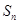 .
.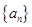 中,
中,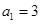 ,前三项的和为
,前三项的和为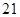 ,则
,则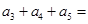 ( )
( )



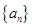 与公比为
与公比为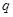 的等比数列
的等比数列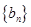 有相同的首项,同时满足
有相同的首项,同时满足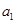 ,
,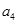 ,
,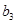 成等比,
成等比,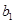 ,
,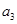 ,
,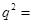 ( )
( )



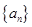 是各项均为正数的等比数列,
是各项均为正数的等比数列,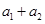 =1,
=1,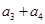 =4,则
=4,则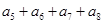 =( )
=( )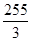
 ,
,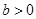 ,且
,且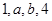 构成等比数列,则 )
构成等比数列,则 )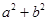 有最小值4
有最小值4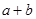 有最小值4
有最小值4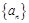 中,
中,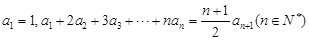
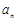 ;
;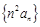 的前
的前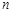 项和
项和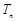 ;
;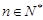 ,使得
,使得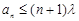 成立,求实数
成立,求实数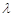 的最小值.
的最小值.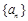 满足
满足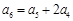 ,则
,则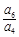 的值为( )
的值为( )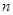 项和为54,前
项和为54,前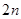 项和为60,则前
项和为60,则前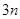 项和为( )
项和为( )


