题目内容
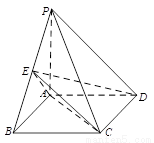
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=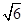 ,点E是棱PB的中点.
,点E是棱PB的中点.
(Ⅰ) 求直线AD与平面PBC的距离;
(Ⅱ) 若AD= ,求二面角A-EC-D的平面角的余弦值.
,求二面角A-EC-D的平面角的余弦值.
【答案】
(1)
(2)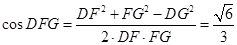
【解析】(1)用传统方法求距离,先要作出表示距离的线段,然后归结为解三角形问题;(2)求二面角时,要掌握“一作二证三求解”的步骤(或者用向量法也行)
(I)在矩形ABCD中,AD//BC,从而AD//平面PBC,故直线AD与平面PBC的距离为点A到平面PBC的距离.因PA⊥底面ABCD,故PA⊥AB,由PA=AB知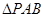 为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB
为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB
又在矩形ABCD中,BC⊥AB,而AB是PB在底面ABCD内的射影,由三垂线定理得BC⊥PB,从而BC⊥平面PAB,故BC⊥AE,从而AE⊥平面PBC,故AE之长即为直线AD与平面PBC的距离.
在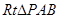 中,PA=AB=
中,PA=AB=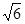 ,所以
,所以
(II)过点D作DF⊥CE,交CE于F,过点F作FG⊥CE,交AC于G,则 为所求的二面角的平面角.由(I)知BC⊥平面PAB,又AD//BC,得AD⊥平面PAB,
为所求的二面角的平面角.由(I)知BC⊥平面PAB,又AD//BC,得AD⊥平面PAB,
故AD⊥AE,从而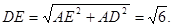
在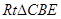 中,
中,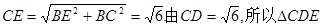 为等边三角形,故F为CE的中点,且
为等边三角形,故F为CE的中点,且
因为AE⊥平面PBC,故AE⊥CE,又FG⊥CE,知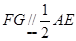 ,从而
,从而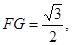 且G点为AC的中点.连接DG,则在
且G点为AC的中点.连接DG,则在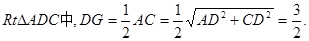
所以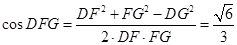

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB. 如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E.
如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.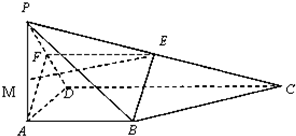 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=