题目内容
已知x∈R，a∈R，a为常数，且f（x+a）=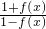
，则函数f（x）必有一周期为
- A.2a
- B.3a
- C.4a
- D.5a
C
分析：根据周期函数的定义，f（x+T）=f（x），T周期，依次计算f（x+na）（n∈N+）直到等于f（x）为止．
解答：∵x∈R，a∈R，a为常数，且f（x+a）=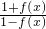
∴f（x+2a）=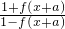
=
，
∴f（x+3a）=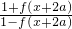
=
，
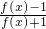∴f（x+4a）=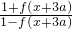
=f（x）；
∴f（x）的周期为4a．
故选C．
点评：本题考查了抽象函数的周期性，利用周期函数的定义求解，一定要抓牢基础．
分析：根据周期函数的定义，f（x+T）=f（x），T周期，依次计算f（x+na）（n∈N+）直到等于f（x）为止．
解答：∵x∈R，a∈R，a为常数，且f（x+a）=
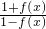
∴f（x+2a）=
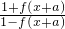=，∴f（x+3a）=
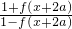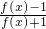=，∴f（x+4a）=
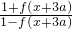=f（x）；∴f（x）的周期为4a．
故选C．
点评：本题考查了抽象函数的周期性，利用周期函数的定义求解，一定要抓牢基础．
练习册系列答案
相关题目
已知x∈R，a∈R，a为常数，且f（x+a）=
，则函数f（x）必有一周期为（ ）
| 1+f(x) |
| 1-f(x) |
| A、2a | B、3a | C、4a | D、5a |
＝(acos2x，1)，
＝(2，
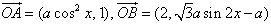asin2x－a)，f(x)＝
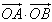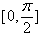]时，f(x)的最大值为5，求a的值．
]上恒成立，求实数m的取值范围．
，f（x）=
，
时，f（x）的最大值为5，求a的值；
上恒成立，求实数m的取值范围。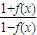 
，则函数f（x）必有一周期为（ ）