题目内容
已知x∈R，a∈R且a≠0，向量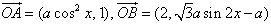
，f（x）=
，
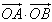（Ⅰ）求函数f（x）的解析式，并求当a>0时，f（x）的单调递增区间；
（Ⅱ）当x∈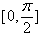
时，f（x）的最大值为5，求a的值；
（Ⅲ）当a=1时，若不等式|f（x）-m|＜2在x∈
上恒成立，求实数m的取值范围。
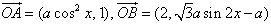，f（x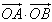）=，（Ⅰ）求函数f（x）的解析式，并求当a>0时，f（x）的单调递增区间；
（Ⅱ）当x∈
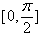时，f（x）的最大值为5，求a的值；（Ⅲ）当a=1时，若不等式|f（x）-m|＜2在x∈
上恒成立，求实数m的取值范围。 解：（Ⅰ）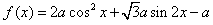
，
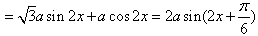因a＞0，由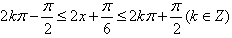
得增区间是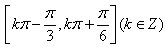
；
（Ⅱ）
，
当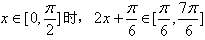
，
若a＞0，当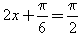
时，f（x）最大值为2a=5，则
；
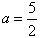若a＜0，当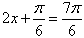
时，f（x）的最大值为-a=5，则a=-5；
综上，a=-5或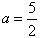
；
（Ⅲ）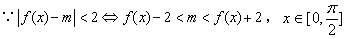
，
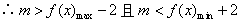，0＜m＜1，
即m的取值范围是（0，1）。
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
已知x∈R，a∈R，a为常数，且f（x+a）=
，则函数f（x）必有一周期为（ ）
| 1+f(x) |
| 1-f(x) |
| A、2a | B、3a | C、4a | D、5a |
＝(acos2x，1)，
＝(2，
asin2x－a)，f(x)＝
]时，f(x)的最大值为5，求a的值．
]上恒成立，求实数m的取值范围．
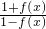，则函数f（x）必有一周期为
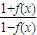，则函数f（x）必有一周期为（ ）