题目内容
已知x∈R，a∈R且a≠0，向量
＝(acos2x，1)，
＝(2，
asin2x－a)，f(x)＝·．
(Ⅰ)求函数f(x)的解析式，并求当a＞0时，f(x)的单调递增区间；
(Ⅱ)当x∈[0，
]时，f(x)的最大值为5，求a的值．
(Ⅲ)当a＝1时，若不等式|f(x)－m|＜2在x∈[0，
]上恒成立，求实数m的取值范围．
答案：
解析：
解析：
|
解：(Ⅰ) 因a＞0，由 (Ⅱ) 若 若 综上， (Ⅲ) |
． 4分
得增区间是
6分
，当
时，
．
最大值为
，则
．
的最大值为
，则
，
且
，
，即
的取值范围是
． 12分
练习册系列答案
名校课堂系列答案
相关题目
已知x∈R，a∈R，a为常数，且f（x+a）=
，则函数f（x）必有一周期为（ ）
| 1+f(x) |
| 1-f(x) |
| A、2a | B、3a | C、4a | D、5a |
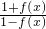，则函数f（x）必有一周期为
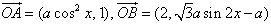，f（x）=
，
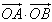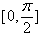时，f（x）的最大值为5，求a的值；
上恒成立，求实数m的取值范围。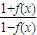 
，则函数f（x）必有一周期为（ ）