题目内容
已知二次函数f(x)的二次项系数为a,且不等式f(x)>2x的解集为(-1,3).(1)若函数g(x)=x,f(x)在区间(-∞,
 )内单调递减,求a的取值范围;
)内单调递减,求a的取值范围;(2)当a=-1时,证明方程f(x)=2x3-1仅有一个实数根.
(3)当x∈[0,1]时,试讨论|f(x)+(2a-1)x+3a+1|≤3成立的充要条件.
【答案】分析:(1)依据不等式f(x)>2x的解集为(-1,3),可设函数f(x)-2x的解析式为(x)-2x=a(x+1)(x-3),得出f(x)的解析式.根据若函数g(x)区间  内单调递减,通过导函数g′(x)<0,求a的取值范围.
内单调递减,通过导函数g′(x)<0,求a的取值范围.
(2)若方程f(x)=2x3-1仅有一个实数根,我们可以构造函数h(x)=2x3+x2-4x-4,则函数h(x)=2x3+x2-4x-4无极值点,或两个极值点的函数值同号,求出函数的导函数,分析后,即可得到结论;
(3)构造函数r(x)=f(x)+(2a-1)x+3a+1,根据二次函数的图象与性质,分析后构造关于a的不等式组,即可求出|f(x)+(2a-1)x+3a+1|≤3成立的充要条件.
解答:解:(1)∵f(x)-2x>0的解集为(-1,3),
∴可设f(x)-2x=a(x+1)(x-3),且a<0,
因而f(x)=a(x+1)(x-3)+2x=ax2+2(1-a)x-3a①
g(x)=xf(x)=ax3+2(1-a)x2-3ax,
∵g(x)在区间 内单调递减,
内单调递减,
∴g′(x)=3ax2+4(1-a)x-3a在 上的函数值非正,
上的函数值非正,
由于a<0,对称轴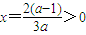 ,
,
故
注意到a<0,∴a2+4(1-a)-9≥0,
得a≤-1或a≥5(舍去)
故所求a的取值范围是(-∞,-1].
(2)当a=-1时,方程f(x)=2x3-1仅有一个实数根,即证方程2x3+x2-4x-4有且仅有一个实数根.
令h(x)=2x3+x2-4x-4,
由h′(x)=6x2+2x-4=0,得x=-1,或x=
由此易得函数h(x)=2x3+x2-4x-4在区间(-∞,-1),( ,+∞)上单调递增,在区间(-1,
,+∞)上单调递增,在区间(-1, )上递减
)上递减
h(x)的极大值h(-1)=-1<0
故函数h(x)的图象与x轴仅有一个交点,
∴当a=-1时,方程f(x)=2x3-1仅有一个实数根
(3)设r(x)=f(x)+(2a-1)x+3a+1=ax2+x+1,
r(0)=1,对称轴为x=
由题意,得 或
或
解得-5≤a<0
故使|f(x)+(2a-1)x+3a+1|≤3成立的充要条件为-5≤a<0
点评:本题考查的知识点是根的存在性及根的个数判断,函数单调性的性质,及二次函数的性质,待定系数法求函数的解析式.步骤一般是首先确定所求问题含待定系数的解析式.其次根据恒等条件,列出一组含待定系数的方程.最后解方程或消去待定系数,从而使问题得到解决.其中熟练掌握二次函数、二次不等式、二次方程之间的联系,熟练的进行相互转化是解答本题的关键.
 内单调递减,通过导函数g′(x)<0,求a的取值范围.
内单调递减,通过导函数g′(x)<0,求a的取值范围.(2)若方程f(x)=2x3-1仅有一个实数根,我们可以构造函数h(x)=2x3+x2-4x-4,则函数h(x)=2x3+x2-4x-4无极值点,或两个极值点的函数值同号,求出函数的导函数,分析后,即可得到结论;
(3)构造函数r(x)=f(x)+(2a-1)x+3a+1,根据二次函数的图象与性质,分析后构造关于a的不等式组,即可求出|f(x)+(2a-1)x+3a+1|≤3成立的充要条件.
解答:解:(1)∵f(x)-2x>0的解集为(-1,3),
∴可设f(x)-2x=a(x+1)(x-3),且a<0,
因而f(x)=a(x+1)(x-3)+2x=ax2+2(1-a)x-3a①
g(x)=xf(x)=ax3+2(1-a)x2-3ax,
∵g(x)在区间
 内单调递减,
内单调递减,∴g′(x)=3ax2+4(1-a)x-3a在
 上的函数值非正,
上的函数值非正,由于a<0,对称轴
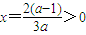 ,
,故

注意到a<0,∴a2+4(1-a)-9≥0,
得a≤-1或a≥5(舍去)
故所求a的取值范围是(-∞,-1].
(2)当a=-1时,方程f(x)=2x3-1仅有一个实数根,即证方程2x3+x2-4x-4有且仅有一个实数根.
令h(x)=2x3+x2-4x-4,
由h′(x)=6x2+2x-4=0,得x=-1,或x=

由此易得函数h(x)=2x3+x2-4x-4在区间(-∞,-1),(
 ,+∞)上单调递增,在区间(-1,
,+∞)上单调递增,在区间(-1, )上递减
)上递减h(x)的极大值h(-1)=-1<0
故函数h(x)的图象与x轴仅有一个交点,
∴当a=-1时,方程f(x)=2x3-1仅有一个实数根
(3)设r(x)=f(x)+(2a-1)x+3a+1=ax2+x+1,
r(0)=1,对称轴为x=

由题意,得
 或
或
解得-5≤a<0
故使|f(x)+(2a-1)x+3a+1|≤3成立的充要条件为-5≤a<0
点评:本题考查的知识点是根的存在性及根的个数判断,函数单调性的性质,及二次函数的性质,待定系数法求函数的解析式.步骤一般是首先确定所求问题含待定系数的解析式.其次根据恒等条件,列出一组含待定系数的方程.最后解方程或消去待定系数,从而使问题得到解决.其中熟练掌握二次函数、二次不等式、二次方程之间的联系,熟练的进行相互转化是解答本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目