题目内容
已知a,b为两个正数,且a>b,设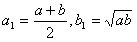 ,当n≥2,n∈N*时,
,当n≥2,n∈N*时,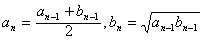 。
。
(1)求证:数列{an}是递减数列,数列{bn}是递增数列;
(2)求证:an+1-bn+1< ;
;
(3)是否存在常数C>0,使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由。
解:(1)证明:易知对任意n∈N*,an>0,bn>0
由a≠b,可知 ,即a1>b1
,即a1>b1
同理, ,即a2>b2
,即a2>b2
可知对任意n∈N*,an>bn
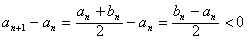
所以数列{an}是递减数列
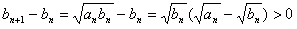
所以数列{bn}是递增数列。
(2)证明: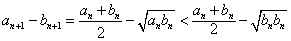
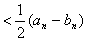 。
。
(3)由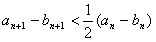
可得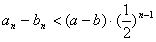
若存在常数C>0,使得对任意n∈N*,有|an-bn|>C,
则对任意n∈N*,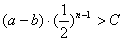
即 对任意n∈N*成立,
对任意n∈N*成立,
即 对任意n∈N*成立,
对任意n∈N*成立,
设[x]表示不超过x的最大整数,
则有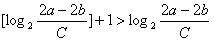
即当 时,
时,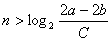
与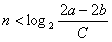 对任意n∈N*成立矛盾
对任意n∈N*成立矛盾
所以,不存在常数C>0,使得对任意n∈N*,有|an-bn|>C。
由a≠b,可知
 ,即a1>b1
,即a1>b1同理,
 ,即a2>b2
,即a2>b2可知对任意n∈N*,an>bn
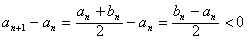
所以数列{an}是递减数列
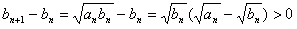
所以数列{bn}是递增数列。
(2)证明:
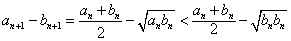
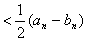 。
。(3)由
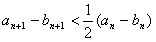
可得
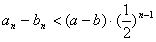
若存在常数C>0,使得对任意n∈N*,有|an-bn|>C,
则对任意n∈N*,
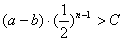
即
 对任意n∈N*成立,
对任意n∈N*成立,即
 对任意n∈N*成立,
对任意n∈N*成立,设[x]表示不超过x的最大整数,
则有
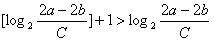
即当
 时,
时,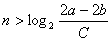
与
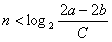 对任意n∈N*成立矛盾
对任意n∈N*成立矛盾所以,不存在常数C>0,使得对任意n∈N*,有|an-bn|>C。

练习册系列答案
相关题目
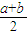 ,b1=
,b1=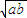 ,当n≥2,n∈N*时,an=
,当n≥2,n∈N*时,an=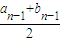 ,bn=
,bn=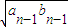 .
. (an-bn);
(an-bn);