Question

如图，已知A、B为两定点，且|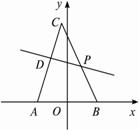|=2c,C为动点且满足||=2a(a＞c＞0,a、c为常数)，D为AC中点，P在边BC上且·=0.

（1）以AB所在直线为x轴，AB中点为坐标原点，建立如图所示的平面直角坐标系，求点P的轨迹方程.

（2）若F、G是点P的轨迹上任意两个不同的点，且线段FG的中垂线与直线AB相交，交点为Q（t,0）.

①证明：存在最小的正数M，使得t＜M,并求M的值.

②若M=，求∠APC的取值范围.

Answer 1

解：（1）∵,?

∴?

根据椭圆定义可知P的轨迹方程为：?

(其中b²=a²-c²,b＞0)?

(2)①设G（x₁ ,y₁）,F(x ₂ ,y ₂),GF的中点（x ₀ ,y ₀）,斜率为k,?

则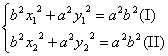

(Ⅰ)-(Ⅱ)得b²x₀+a²y₀k=0.?

若k=0,则FG的中垂线为y轴t=0；?

若k≠0，则-=.?

GF的中垂线方程为y-y₀=(x-x₀)，则-y₀=(t-x₀),t=-+x₀-x₀ .?

∵FG的中垂线与AB直线相交，?

∴-a＜x₀＜a,∴-.?

∴存在最小正数M=,使得t＜M.?

②∵M=,∴,.?

设∠APB=θ,||=r₁ ,||=r₂ ,?

∴r₁+r₂=2a,?

∴.

∴0°≤θ≤60°,∴∠APC∈(120°,180°］.