题目内容
已知a,b为两个正数,且a>b,设a1=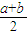 ,b1=
,b1=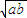 ,当n≥2,n∈N*时,an=
,当n≥2,n∈N*时,an=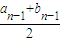 ,bn=
,bn=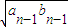 .
.(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1<
 (an-bn);
(an-bn);(Ⅲ)是否存在常数C>0使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由.
【答案】分析:(I)易知对任意n∈N*,an>0,bn>0.根据基本不等式可知对任意n∈N*,an>bn, 判定符号可得数列{an}的单调性,
判定符号可得数列{an}的单调性,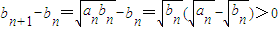 ,从而得到数列{bn}的单调性;
,从而得到数列{bn}的单调性;
(II)根据题意可知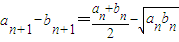 ,然后利用放缩法即可证得结论;
,然后利用放缩法即可证得结论;
(III)若存在常数C>0使得对任意n∈N*,有|an-bn|>C,则对任意n∈N*,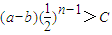 ,即
,即 对任意n∈N*成立,设[x]表示不超过x最大整数,则有
对任意n∈N*成立,设[x]表示不超过x最大整数,则有 ,即当
,即当 时,
时,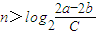 与
与 对任意n∈N*成立矛盾.从而所以,不存在常数C>0使得对任意n∈N*,有|an-bn|>C.
对任意n∈N*成立矛盾.从而所以,不存在常数C>0使得对任意n∈N*,有|an-bn|>C.
解答:(共13分)
(Ⅰ)证明:易知对任意n∈N*,an>0,bn>0.
由a≠b,可知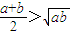 ,即a1>b1.
,即a1>b1.
同理,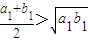 ,即a2>b2.
,即a2>b2.
可知对任意n∈N*,an>bn.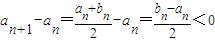 ,
,
所以数列{an}是递减数列.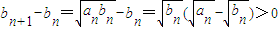 ,
,
所以数列{bn}是递增数列. …(5分)
(Ⅱ)证明: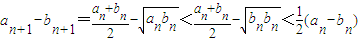 .…(10分)
.…(10分)
(Ⅲ)解:由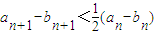 ,可得
,可得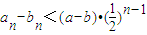 .
.
若存在常数C>0使得对任意n∈N*,有|an-bn|>C,
则对任意n∈N*,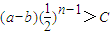 .
.
即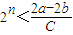 对任意n∈N*成立.
对任意n∈N*成立.
即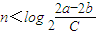 对任意n∈N*成立.
对任意n∈N*成立.
设[x]表示不超过x最大整数,则有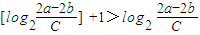 .
.
即当 时,
时,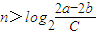 .
.
与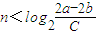 对任意n∈N*成立矛盾.
对任意n∈N*成立矛盾.
所以,不存在常数C>0使得对任意n∈N*,有|an-bn|>C. …(14分)
点评:本题主要考查了数列的单调性的判定,以及利用放缩法证明不等式,同时考查了横成立问题,属于难题.
 判定符号可得数列{an}的单调性,
判定符号可得数列{an}的单调性,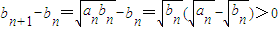 ,从而得到数列{bn}的单调性;
,从而得到数列{bn}的单调性; (II)根据题意可知
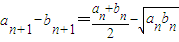 ,然后利用放缩法即可证得结论;
,然后利用放缩法即可证得结论;(III)若存在常数C>0使得对任意n∈N*,有|an-bn|>C,则对任意n∈N*,
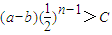 ,即
,即 对任意n∈N*成立,设[x]表示不超过x最大整数,则有
对任意n∈N*成立,设[x]表示不超过x最大整数,则有 ,即当
,即当 时,
时,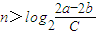 与
与 对任意n∈N*成立矛盾.从而所以,不存在常数C>0使得对任意n∈N*,有|an-bn|>C.
对任意n∈N*成立矛盾.从而所以,不存在常数C>0使得对任意n∈N*,有|an-bn|>C.解答:(共13分)
(Ⅰ)证明:易知对任意n∈N*,an>0,bn>0.
由a≠b,可知
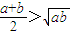 ,即a1>b1.
,即a1>b1.同理,
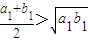 ,即a2>b2.
,即a2>b2.可知对任意n∈N*,an>bn.
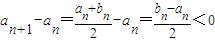 ,
,所以数列{an}是递减数列.
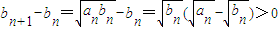 ,
,所以数列{bn}是递增数列. …(5分)
(Ⅱ)证明:
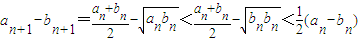 .…(10分)
.…(10分)(Ⅲ)解:由
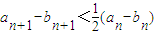 ,可得
,可得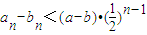 .
.若存在常数C>0使得对任意n∈N*,有|an-bn|>C,
则对任意n∈N*,
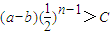 .
.即
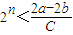 对任意n∈N*成立.
对任意n∈N*成立.即
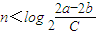 对任意n∈N*成立.
对任意n∈N*成立.设[x]表示不超过x最大整数,则有
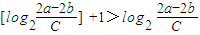 .
.即当
 时,
时,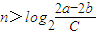 .
.与
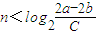 对任意n∈N*成立矛盾.
对任意n∈N*成立矛盾.所以,不存在常数C>0使得对任意n∈N*,有|an-bn|>C. …(14分)
点评:本题主要考查了数列的单调性的判定,以及利用放缩法证明不等式,同时考查了横成立问题,属于难题.

练习册系列答案
相关题目
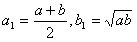 ,当n≥2,n∈N*时,
,当n≥2,n∈N*时,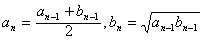 。
。 ;
;