题目内容
(2013•汕头二模)关于二项式(x-1)2013有下列命题:
(1)该二项展开式中非常数项的系数和是1;
(2)该二项展开式中第六项为
x2007;
(3)该二项展开式中系数最大的项是第1007项;
(4)当x=2014时,(x-1)2013除以2014的余数是2013.
其中正确命题有( )
(1)该二项展开式中非常数项的系数和是1;
(2)该二项展开式中第六项为
| C | 6 2013 |
(3)该二项展开式中系数最大的项是第1007项;
(4)当x=2014时,(x-1)2013除以2014的余数是2013.
其中正确命题有( )
分析:利用赋值求出各项系数和,判断出命题(1)正确;利用二项展开式的通项公式求出第六项,判断出命题(2)错误;据二项展开式的二项式系数的性质:中间项的二项式系数最大,判断出命题(3)正确;利用二项式定理将二项式展开,判断出命题(4)正确.
解答:解:此二项展开式各项系数的和为0,其常数项为-1,故(1)正确;
其第六项T6=C20135x2013-5•(-1)5=-C20135x2008,故(2)错;
该二项展开式共有2014项,奇数项系数为正、偶数项系数为负,
由二项式系数的性质知第1007项与1008项系数的绝对值最大,故(3)正确;
(x-1)2013=(x2013-C20131x2012+C20132x2011-…+C20132012x)-1=(x2013-C20131x2012+C20132x2011-…+C20132012-1)x+x-1.当x=2014时,被2014除的余数为2014-1=2013.故(4)正确.
其中正确命题有3个.
故选C.
其第六项T6=C20135x2013-5•(-1)5=-C20135x2008,故(2)错;
该二项展开式共有2014项,奇数项系数为正、偶数项系数为负,
由二项式系数的性质知第1007项与1008项系数的绝对值最大,故(3)正确;
(x-1)2013=(x2013-C20131x2012+C20132x2011-…+C20132012x)-1=(x2013-C20131x2012+C20132x2011-…+C20132012-1)x+x-1.当x=2014时,被2014除的余数为2014-1=2013.故(4)正确.
其中正确命题有3个.
故选C.
点评:本题考查求展开式的系数和的方法是赋值法,考查二项展开式的通项公式解决展开式的特定项问题,考查展开式的二项式系数的性质.属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为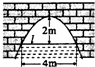 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽