题目内容
正方形ABCD在直角坐标平面内,已知其一条边AB在直线y=x+4上,C,D在抛物线x=y2上,求正方形ABCD的面积.
分析:根据C,D两点在抛物线上可设出C,D的坐标,根据直线A,B的方程可知AB与y轴成的夹角,进而推断出角线AC与边AB也成450角,进而推断出AC∥y轴,和BD∥x轴,设出A,B的坐标,根据AB∥CD,对角线AC,BD互相垂直平分,联立方程求得s和t,则正方形ABCD的面积可求得.
解答:解:∵C,D两点在抛物线上,
∴可设C(s2,s),D(t2,,t),
又∵A,B在直线y=x+4上,∴AB与y轴成450角,
∵四边形ABCD为正方形,
∴对角线AC与边AB也成450角,
∴AC∥y轴,同理BD∥x轴,
∴可设A(s2,s2+4),B(t-4,t)
∵AB∥CD,对角线AC,BD互相垂直平分,所以有
解得
∴面积S1=|C1D1|2=[(-1)2-22]2+[(-1)-2]2=18,
S2=|C2D2|2=[(-1)2-32]2+[(-1)-3]2=50.
答:这样的正方形有两个,其面积分别为18,50.
∴可设C(s2,s),D(t2,,t),
又∵A,B在直线y=x+4上,∴AB与y轴成450角,
∵四边形ABCD为正方形,
∴对角线AC与边AB也成450角,
∴AC∥y轴,同理BD∥x轴,
∴可设A(s2,s2+4),B(t-4,t)
∵AB∥CD,对角线AC,BD互相垂直平分,所以有
|
|
|
∴面积S1=|C1D1|2=[(-1)2-22]2+[(-1)-2]2=18,
S2=|C2D2|2=[(-1)2-32]2+[(-1)-3]2=50.
答:这样的正方形有两个,其面积分别为18,50.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生的分析推理和数形结合思想的灵活运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
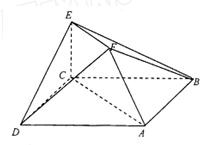 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=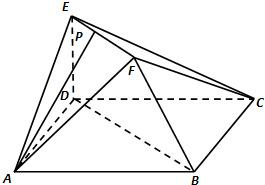 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=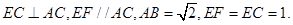
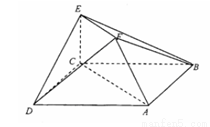
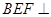 平面DEF;
平面DEF;