题目内容
在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心．点P在棱CC1上，且CC1=4CP．（1）设O点在平面D1AP上的射影是H，求证：D1H⊥AP；
（2）求V锥P-ABD1．
分析：（1）连接A1C1，利用O点在平面D1AP上的射影是H，通过证明AP⊥面D1OH，然后证明D1H⊥AP；
（2）直接通过转化利用V锥P-ABD1=VQ-ABD1=VB-D1QA，求解V锥P-ABD1．
（2）直接通过转化利用V锥P-ABD1=VQ-ABD1=VB-D1QA，求解V锥P-ABD1．
解答：解：（1）证明：连接A1C1
∵正方体AC1∴O为A1C1的中点∴D1O⊥A1C1
又 A1A⊥面A1B1C1D1∴A1A⊥D1O∴D1O⊥面A1ACC1
AP?面A1ACC1∴D1O⊥AP
由已知OH⊥面AD1P∴OH⊥AP
∴AP⊥面D1OH，又D1H?面D1OH
∴AP⊥D1H（6分）
（2）解：在DD1上取点Q，使DQ=1
∴DQ
CP∴PQ
CD
又CD
AB∴PQ
AB
AB?面ABD1，PQ?面ABD1
∴PQ∥面ABD1
∴V锥P-ABD1=VQ-ABD1=VB-D1QA=
•
•3•4•4=8（12分）
∵正方体AC1∴O为A1C1的中点∴D1O⊥A1C1
又 A1A⊥面A1B1C1D1∴A1A⊥D1O∴D1O⊥面A1ACC1
AP?面A1ACC1∴D1O⊥AP
由已知OH⊥面AD1P∴OH⊥AP
∴AP⊥面D1OH，又D1H?面D1OH
∴AP⊥D1H（6分）
（2）解：在DD1上取点Q，使DQ=1
∴DQ
| ||
. |
| ||
. |
又CD
| ||
. |
| ||
. |
AB?面ABD1，PQ?面ABD1
∴PQ∥面ABD1
∴V锥P-ABD1=VQ-ABD1=VB-D1QA=
| 1 |
| 3 |
| 1 |
| 2 |
点评：本题考查直线与平面垂直的性质的应用，几何体的体积的求法，考查逻辑推理能力与计算能力．
练习册系列答案
相关题目
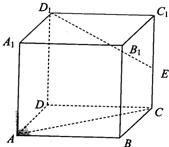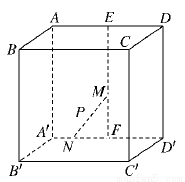
如图所示，在棱长为4的正方体ABCD-A1B1C1D1中，点E是棱CC1的中点．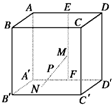
如图，在棱长为4的正方体ABCD-A′B′C′D′中，E、F分别是AD、A′D′的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A′B′C′D′上运动，则线段MN的中点P的轨迹（曲面）与二面角A-A′D′-B′所围成的几何体的体积为（ ）
在棱长为4的正方体ABCD-A1B1C1D1中，点E、F分别在棱AA1和AB上，且C1E⊥EF，则|AF|的最大值为（ ）
