题目内容
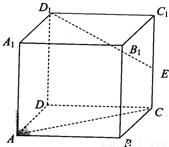
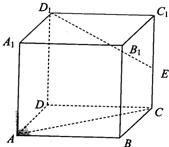 如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点.
如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点.(I)求三棱锥D1-ACE的体积;
(II)求异面直线D1E与AC所成角的余弦值;
(III)求二面角A-D1E-C的正弦值.
分析:(I)利用VD1-ACE=VA-D1CE,求出底面D1CE的面积,然后求三棱锥D1-ACE的体积;
(II)取DD1的中点F,连接FC,说明∠FCA即为异面直线D1E与AC所成角或其补角,解三角形CEF,求异面直线D1E与AC所成角的余弦值;
(III)过点D作DG⊥D1E于点G,连接AG,说明∠AGD为二面角A-D1E-C的平面角,解△AGD,求二面角A-D1E-C的正弦值.
(II)取DD1的中点F,连接FC,说明∠FCA即为异面直线D1E与AC所成角或其补角,解三角形CEF,求异面直线D1E与AC所成角的余弦值;
(III)过点D作DG⊥D1E于点G,连接AG,说明∠AGD为二面角A-D1E-C的平面角,解△AGD,求二面角A-D1E-C的正弦值.
解答:解:(I)VD1-ACE=VA-D1CE=
×
×2×3×3=
(II)取DD1的中点F,连接FC,
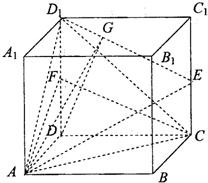
则D1E∥FC,
∴∠FCA即为异面直线D1E与AC
所成角或其补角.
在△FCA中,AC=4
,
AF=FC=2
∴cos∠FCA=
∴异面直线D1E与AC所成角的余弦值为
.
(III)过点D作DG⊥D1E于点G,连接AG,由AD⊥面D1DCC1,
∴AD⊥D2E
又∵DG⊥D1E,∴D1E⊥面ADG
∴D1E⊥AG,则∠AGD为二面角A-D1E-C的平面角
∵D1E•DG=DD1•CD,∴DG=
AG=
=
∴sin∠AGD=
,
二面角A-D1E-C的正弦值为
.
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
(II)取DD1的中点F,连接FC,

则D1E∥FC,
∴∠FCA即为异面直线D1E与AC
所成角或其补角.
在△FCA中,AC=4
| 2 |
AF=FC=2
| 5 |
∴cos∠FCA=
| ||
| 5 |
∴异面直线D1E与AC所成角的余弦值为
| ||
| 5 |
(III)过点D作DG⊥D1E于点G,连接AG,由AD⊥面D1DCC1,
∴AD⊥D2E
又∵DG⊥D1E,∴D1E⊥面ADG
∴D1E⊥AG,则∠AGD为二面角A-D1E-C的平面角
∵D1E•DG=DD1•CD,∴DG=
8
| ||
| 5 |
| AD2+DG2 |
12
| ||
| 5 |
∴sin∠AGD=
| ||
| 3 |
二面角A-D1E-C的正弦值为
| ||
| 3 |
点评:本题考查棱柱、棱锥、棱台的体积,异面直线及其所成的角,二面角及其度量,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目