题目内容
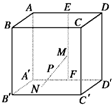 如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )分析:直接根据条件得到点P的轨迹是以点F为球心、1为半径的球面,进而求出结论.
解答:解:依题意可知|FP|=
|MN|=1,
因此点P的轨迹是以点F为球心、1为半径的球面的
.
于是所求的体积是
×(
π×13)=
π.
故选:C.
| 1 |
| 2 |
因此点P的轨迹是以点F为球心、1为半径的球面的
| 1 |
| 4 |
于是所求的体积是
| 1 |
| 4 |
| 4 |
| 3 |
| 1 |
| 3 |
故选:C.
点评:解决此类问题的关键是熟悉结合体的结构特征与球的定义以及其表面积的计算公式.考查空间想象能力,计算能力.

练习册系列答案
相关题目
 (2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )
(2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( ) 如图,正方体ABCD-A1B1C1D1的棱长为4,点P从B点出发,在正方形BCC1B1的边上按逆针方向按如下规律运动:设第n次运动的路程为an,且
如图,正方体ABCD-A1B1C1D1的棱长为4,点P从B点出发,在正方形BCC1B1的边上按逆针方向按如下规律运动:设第n次运动的路程为an,且 如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点.
如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点. (2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是
(2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是 平面
平面 ,垂足为
,垂足为 ,正四面体
,正四面体 的棱长为4,
的棱长为4, 在平面
在平面 是直线
是直线 上的动点,则当
上的动点,则当 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面 B.
B. C.
C. D.
D.
