题目内容
(本题满分14分,第1小题6分,第2小题8分)
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE。
(1)求证:AE⊥BC;
(2)如果点N为线段AB的中点,求证:MN∥平面ADE.
 |
【答案】
(本题满分14分,第1小题6分,第2小题8分)
证明:⑴因为BM⊥平面ACE,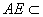 平面
平面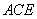 ,
,
所以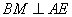 .……………2分
.……………2分
因为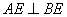 ,且
,且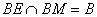 ,
,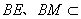 平面EBC,
平面EBC,
所以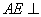 平面EBC.……………………………………………………………………4分
平面EBC.……………………………………………………………………4分
因为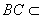 平面EBC,所以
平面EBC,所以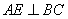 .………………………………………………6分
.………………………………………………6分
⑵取DE中点H,连结MH、AH.
因为BM⊥平面ACE,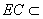 平面
平面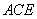 ,所以
,所以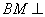
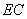 .
.
因为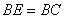 ,所以M为CE的中点.………………………………………………8分
,所以M为CE的中点.………………………………………………8分
所以MH为△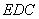 的中位线.所以
的中位线.所以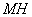 ∥
∥ ,…………10分
,…………10分
因为四边形ABCD为平行四边形,所以DC∥AB,故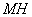 ∥
∥ .
.
因为N为AB中点,所以MH∥AN.
所以四边形ANMH为平行四边形,所以MN∥AH.………………………………12分
因为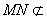 平面ADE,
平面ADE,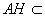 平面ADE,所以MN∥平面ADE.………………14分
平面ADE,所以MN∥平面ADE.………………14分
法二:取EB中点F,连接MF、NF
同法意,可得M为CE中点。
因为N为AB中点,所以NF∥AE,MF∥BC………………………………………8分
因为四边形ABCD为平行四边形,所以AD∥BC,所以MF∥AD。
因为NF、MF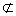 平面ADE,AD、AE
平面ADE,AD、AE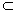 平面MNF,
平面MNF,
所以平面MNF∥平面ADE……10分
因为MF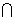 NF=F,MF、NF
NF=F,MF、NF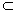 平面MNF,所以平面MNF∥平面ADE…………12分
平面MNF,所以平面MNF∥平面ADE…………12分
因为MN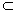 平面MNF,所以MN∥平面ADE………………………………14分
平面MNF,所以MN∥平面ADE………………………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1. ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
 ,若不等式
,若不等式 的解集为
的解集为 。
。 的值;
的值; 在
在 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。