题目内容
在数列{an}中,已知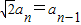 ,且a1=1,则a5=( )
,且a1=1,则a5=( )A.

B.
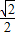
C.

D.
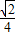
【答案】分析:判断数列是等比数列,直接利用通项公式,求出a5即可.
解答:解:因为数列{an}中,已知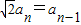 ,且a1=1,
,且a1=1,
所以数列是等比数列,公比为: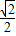 ,
,
所以a5=a1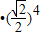 =
= .
.
故选C.
点评:本题考查等比数列通项公式的应用,考查计算能力.
解答:解:因为数列{an}中,已知
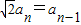 ,且a1=1,
,且a1=1,所以数列是等比数列,公比为:
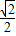 ,
,所以a5=a1
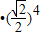 =
= .
.故选C.
点评:本题考查等比数列通项公式的应用,考查计算能力.

练习册系列答案
相关题目