题目内容
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为 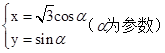 .
.
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为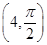 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值;
(Ⅲ)请问是否存在直线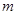 ,
,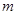 ∥l且
∥l且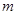 与曲线C的交点A、B满足
与曲线C的交点A、B满足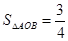 ;
;
若存在请求出满足题意的所有直线方程,若不存在请说明理由。
(Ⅰ)P(0,4),点P在直线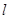 上(Ⅱ)最小值为
上(Ⅱ)最小值为 ,最大值为
,最大值为 (Ⅲ)
(Ⅲ) 或
或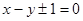
解析试题分析:(I)把极坐标系下的点 化为直角坐标,得P(0,4)2分
化为直角坐标,得P(0,4)2分
因为点P的直角坐标(0,4)满足直线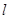 的方程
的方程 ,所以点P在直线
,所以点P在直线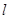 上.4分
上.4分
(II)因为点Q在曲线C上,故可设点Q的坐标为 ,5分
,5分
从而点Q到直线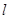 的距离为
的距离为 , 6分
, 6分
由此得,当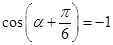 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为
当 时,d取得最大值,且最大值为
时,d取得最大值,且最大值为 8分
8分
(Ⅲ)设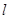 平行线m方程:
平行线m方程: 9分
9分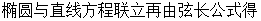
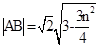
设O到直线m的距离为d,则 10分
10分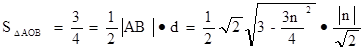
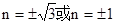 经验证均满足题意 ,所求方程为
经验证均满足题意 ,所求方程为 或
或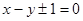 12分
12分
考点:极坐标化直角坐标及平面内直线与椭圆相交相离的位置关系
点评:极坐标 与直角坐标
与直角坐标 的互化
的互化 ,第二问求距离的最值首先找到距离的表达式,借助于三角函数参数的有界性求得最值,第三问是直线与椭圆相交问题,此题求三角形面积用到了弦长,因此联立方程求出弦长得到面积
,第二问求距离的最值首先找到距离的表达式,借助于三角函数参数的有界性求得最值,第三问是直线与椭圆相交问题,此题求三角形面积用到了弦长,因此联立方程求出弦长得到面积

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
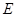 :
: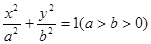 的右焦点
的右焦点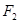 与抛物线
与抛物线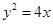 的焦点重合,过
的焦点重合,过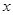 轴垂直的直线
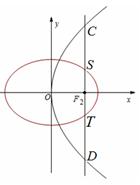
轴垂直的直线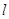 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且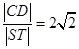 .
.
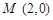 的直线与椭圆
的直线与椭圆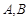 ,设
,设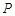 为椭圆
为椭圆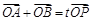 (
( 为坐标原点),当
为坐标原点),当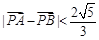 时,求实数
时,求实数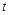 的取值范围.
的取值范围.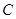 的极坐标方程为
的极坐标方程为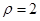 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为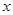 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆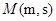 作平行于
作平行于 轴的直线
轴的直线 ,设
,设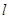 与
与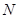 ,向量
,向量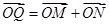 .
.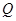 的轨迹方程;
的轨迹方程;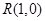 ,求
,求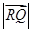 的最小值.
的最小值. 的离心率为
的离心率为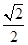 ,且经过点
,且经过点 .
. ,
, 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且 .求△ABM的面积.
.求△ABM的面积.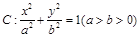 ,直线l为圆
,直线l为圆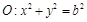 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为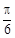 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.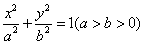 过点
过点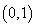 ,其长轴、焦距和短轴的长的平方依次成等差数列.直线
,其长轴、焦距和短轴的长的平方依次成等差数列.直线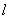 与
与 轴正半轴和
轴正半轴和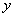 轴分别交于点
轴分别交于点 、
、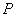 ,与椭圆分别交于点
,与椭圆分别交于点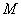 、
、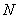 ,各点均不重合且满足
,各点均不重合且满足
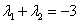 ,试证明:直线
,试证明:直线 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切. 及动圆圆心轨迹
及动圆圆心轨迹 的方程;
的方程; 、
、 ,椭圆
,椭圆 、
、 ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值. 分别是椭圆的
分别是椭圆的 左,右焦点。
左,右焦点。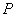 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且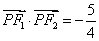 ,求点
,求点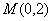 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点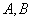 ,且
,且 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线 的斜率
的斜率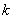 的取值范围。
的取值范围。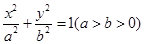 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为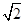 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量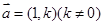 为方向向量的直线
为方向向量的直线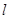 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若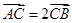 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。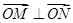 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.