题目内容
如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，AA1=2．底面ABC是边长为2的正三角形，其重心为G点，E是线段BC1上一点，且BE=| 1 | 3 |
（1）求证：GE∥侧面AA1B1B；
（2）求平面B1GE与底面ABC所成锐二面角的正切值；
（3）求点B到平面B1GE的距离．
分析：解法1：（1）根据BE=
BC1，利用相似三角形的比例关系，即可证得直线与直线平行，再运用线面平行的判定定理，即可证得结论；
（2）根据二面角的定义，在两个半平面内各找一条直线垂直于二面角的棱，从而找到二面角的平面角，在三角形中求解，即可得到答案；
解法2：（1）建立空间直角坐标系，求出侧面AA1B1B的法向量和向量
，判断法向量和向量
垂直，即可证得结论；
（2）求出两个半平面的法向量，利用向量的数量积，求出法向量的夹角的余弦值，再利用法向量的夹角与二面角的平面角之间的关系，即可求得答案；
（3）利用点到面的距离，向量
构造直角三角形，再利用向量
与平面B1GE的法向量的夹角，在直角三角形中即可求得B到平面B1GE的距离．
| 1 |
| 3 |
（2）根据二面角的定义，在两个半平面内各找一条直线垂直于二面角的棱，从而找到二面角的平面角，在三角形中求解，即可得到答案；
解法2：（1）建立空间直角坐标系，求出侧面AA1B1B的法向量和向量
| GE |
| GE |
（2）求出两个半平面的法向量，利用向量的数量积，求出法向量的夹角的余弦值，再利用法向量的夹角与二面角的平面角之间的关系，即可求得答案；
（3）利用点到面的距离，向量
| BG |
| BG |
解答：解法1：（1）延长B1E交BC于点F，
∵△B1EC1∽△FEB，且BE=
EC1，
∴BF=
B1C1=
BC，
∴点F为BC的中点，
∵G为△ABC的重心，
∴A、G、F三点共线，且
=
=
，
∴GE∥AB1，
又GE?侧面AA1B1B，AB1?侧面AA1B1B，
∴GE∥侧面AA1B1B；
（2）在侧面AA1B1B内，过B1作B1H⊥AB，垂足为H，
∵侧面AA1B1B⊥底面ABC，
∴B1H⊥底面ABC，
又侧棱AA1与底面ABC成60°的角，AA1=2，
∴∠B1BH=60°，BH=1，B1H=
，
在底面ABC内，过H作HT⊥AF，垂足为T，连B1T，
根据三垂线定理可得，B1T⊥AF，
∵平面B1CE与底面ABC的交线为AF，
∴∠B1TH为所求二面角的平面角，
∴AH=AB+BH=3，∠HAT=30°，
∴HT=AHsin30°=
，
在Rt△B1HT中，tan∠B1TH=
=
，
故平面B1GE与底面ABC成锐二面角的正切值为
；
解法2：（1）∵侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，
∴∠A1AB=60°，
又∵AA1=AB=2，取AB得中点O，则A1O⊥底面ABC，
∴以O为原点，以{
，
，
}为基底，建立空间直角坐标系O-xyz如图所示，
则A（0，-1，0），B（0，1，0），C（
，0，0），A1（0，0，
），B1（0，2，
），C1（
，1，
），
∵G为△ABC的重心，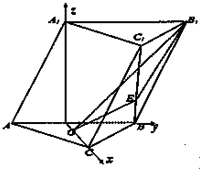
∴G（
，0，0），
∵
=
，
∴E（
，1，
），
∴
=(0，1，
)=
，
又∵GE?侧面AA1B1B，
∴GE∥侧面AA1B1B；
（2）设平面B1GE的法向量为
=(a，b，c)，则由
，可得
，
取
=（
，-1，
），
又底面ABC的一个法向量为
=（0，0，1），
设平面B1GE与底面ABC所成锐二面角的大小为θ，则cosθ=
=
，
∵θ为锐角，
∴sinθ=
=
，
∴tanθ=
；
故平面B1GE与底面ABC成锐二面角的正切值为
；
（3）由（2）可知平面B1GE的法向量为
=（
，-1，
），
=（
，-1，0），
d=
=
=
=
所以点B到平面B1GE的距离为：
．
∵△B1EC1∽△FEB，且BE=
| 1 |
| 2 |
∴BF=
| 1 |
| 2 |
| 1 |
| 2 |
∴点F为BC的中点，
∵G为△ABC的重心，
∴A、G、F三点共线，且
| FG |
| FA |
| FE |
| FB1 |
| 1 |
| 3 |
∴GE∥AB1，
又GE?侧面AA1B1B，AB1?侧面AA1B1B，
∴GE∥侧面AA1B1B；
（2）在侧面AA1B1B内，过B1作B1H⊥AB，垂足为H，
∵侧面AA1B1B⊥底面ABC，
∴B1H⊥底面ABC，
又侧棱AA1与底面ABC成60°的角，AA1=2，
∴∠B1BH=60°，BH=1，B1H=
| 3 |
在底面ABC内，过H作HT⊥AF，垂足为T，连B1T，
根据三垂线定理可得，B1T⊥AF，
∵平面B1CE与底面ABC的交线为AF，
∴∠B1TH为所求二面角的平面角，
∴AH=AB+BH=3，∠HAT=30°，
∴HT=AHsin30°=
| 3 |
| 2 |
在Rt△B1HT中，tan∠B1TH=
| B1H |
| HT |
2
| ||
| 3 |
故平面B1GE与底面ABC成锐二面角的正切值为
2
| ||
| 3 |
解法2：（1）∵侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，
∴∠A1AB=60°，
又∵AA1=AB=2，取AB得中点O，则A1O⊥底面ABC，
∴以O为原点，以{
| OC |
| OB |
| OA1 |
则A（0，-1，0），B（0，1，0），C（
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∵G为△ABC的重心，
∴G（
| ||
| 3 |
∵
| BE |
| 1 |
| 3 |
| BC1 |
∴E（
| ||
| 3 |
| ||
| 3 |
∴
| CE |
| ||
| 3 |
| 1 |
| 3 |
| AB1 |
又∵GE?侧面AA1B1B，
∴GE∥侧面AA1B1B；
（2）设平面B1GE的法向量为
| n |
|
|
取
| n |
| 3 |
| 3 |
又底面ABC的一个法向量为
| m |
设平面B1GE与底面ABC所成锐二面角的大小为θ，则cosθ=
| ||||
|
|
| ||
| 7 |
∵θ为锐角，
∴sinθ=
| 1-cos2θ |
2
| ||
| 7 |
∴tanθ=
2
| ||
| 3 |
故平面B1GE与底面ABC成锐二面角的正切值为
2
| ||
| 3 |
（3）由（2）可知平面B1GE的法向量为
| n |
| 3 |
| 3 |
| BG |
| ||
| 3 |
d=
|
| ||||
|
|
|(
| ||||||||
|(
|
| 2 | ||
|
2
| ||
| 7 |
所以点B到平面B1GE的距离为：
2
| ||
| 7 |
点评：本题考查了直线与平面平行的判定，二面角的平面角的寻找以及相关的求解问题，点、线、面之间距离的计算．在求解二面角的时候，一种方法是找出二面角的平面角，然后在三角形中求解即可，另一种方法是运用空间向量，建立直角坐标系进行求解．而点到面的距离的求解，一种方法是运用等体积法，另一种是运用空间向量进行求解．属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
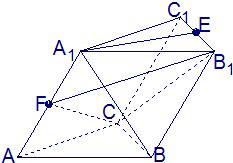如图，在斜三棱柱ABC-A1B1C1中，∠A1AB=∠A1AC，AB=AC，A1A=A1B=a，侧面B1BCC1与底面ABC所成的二面角为120°，E、F分别是棱B1C1、A1A的中点
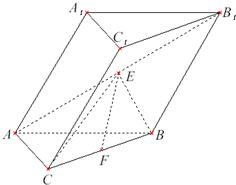如图，在斜三棱柱ABC-A1B1C1中，AC=BC，AC⊥BC．侧面A1ABB1是边长为a的菱形，且垂直于底面ABC，∠A1AB=60°，E，F分别是AB1，BC的中点． 
如图，在斜三棱柱ABC-A1B1C1中，∠BAC=90°，又BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H一定在（ ）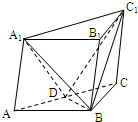
（2007•武汉模拟）如图，在斜三棱柱ABC-A1B1C1中 AB=BC=2，∠ABC=120°，又顶点A1在底面ABC上的射影落在AC上，侧棱AA1与底面成60°的角，D为AC的中点．
（2008•武汉模拟）如图，在斜三棱柱ABC-A'B'C'中，∠ABC=90°，则侧面A'ACC'⊥侧面ABC，又AA'和底面所成60°的角，且AA'=2a，AB=BC=