题目内容
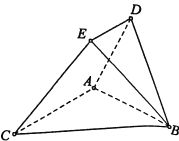
【题目】如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,且满足![]() .
.

(1)求证:四边形EFGH是梯形;
(2)若BD=a,求梯形EFGH的中位线的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)利用比例关系,求出EH∥BD,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,即可证明四边形EFGH是梯形;
BD,即可证明四边形EFGH是梯形;
(2)EH=![]() a,FG=
a,FG=![]() a,即可求梯形EFGH的中位线的长.
a,即可求梯形EFGH的中位线的长.
试题解析:
(1)证明 因为![]() =
=![]() =
=![]() ,
,
所以EH∥BD,且EH=![]() BD.
BD.
因为![]() =
=![]() =2,
=2,
所以FG∥BD,且FG=![]() BD.
BD.
因而EH∥FG,且EH=![]() FG,
FG,
故四边形EFGH是梯形.
(2)解 因为BD=a,所以EH=![]() a,FG=
a,FG=![]() a,所以梯形EFGH的中位线的长为
a,所以梯形EFGH的中位线的长为![]() (EH+FG)=
(EH+FG)=![]() a.
a.

练习册系列答案
相关题目