题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,且
,且![]() .过椭圆的右焦点
.过椭圆的右焦点![]() 作长轴的垂线与椭圆,在第一象限交于点
作长轴的垂线与椭圆,在第一象限交于点![]() ,且满足
,且满足![]() .
.
(1)求椭圆的标准方程;
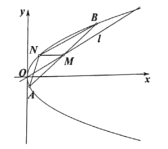
(2)若矩形![]() 的四条边均与椭圆相切,求该矩形面积的取值范围.
的四条边均与椭圆相切,求该矩形面积的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)易知![]() ,设
,设![]() ,
,![]() ,根据勾股定理计算得到
,根据勾股定理计算得到![]() ,得到椭圆方程.
,得到椭圆方程.
(2)考虑矩形边与坐标轴平行和不平行两种情况,联立方程组根据![]() 得到
得到![]() 和
和![]() 的关系,计算边长得到面积表达式,根据均值不等式计算得到答案.
的关系,计算边长得到面积表达式,根据均值不等式计算得到答案.![]()
(1)由![]() ,可知椭圆半焦距
,可知椭圆半焦距![]() ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
在![]() △
△![]() 中,
中,![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]() .
.
(2)记矩形面积为![]() ,当矩形一边与坐标轴平行时,易知
,当矩形一边与坐标轴平行时,易知![]() .
.
当矩形的边与坐标轴不平行时,根据对称性,设其中一边所在直线方程为![]() ,
,
则对边所在直线方程为![]() ,
,
另一边所在的直线方程为![]() ,则对边所在直线方程为
,则对边所在直线方程为![]() ,
,
联立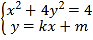 ,得
,得![]() ,
,
由题意知![]() ,整理得
,整理得![]() ,
,
矩形的一边长为![]() ,同理
,同理![]() ,矩形的另一边长为
,矩形的另一边长为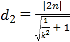 ,
,
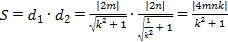
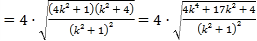
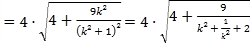 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
所以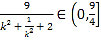 ,则
,则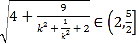 ,所以
,所以![]() .
.
综上所述,该矩形面积的取值范围为![]() .
.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
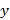
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中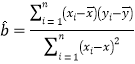
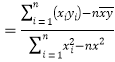 .
.
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中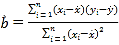 ,
,![]() .相关系数
.相关系数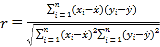 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()