题目内容
【题目】动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离的比值为
的距离的比值为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于两点
交于两点![]() ,
,![]() ,设点
,设点![]() ,
,![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)设![]() 的坐标为
的坐标为![]() ,由题意可得等式
,由题意可得等式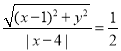 ,整理可得动点
,整理可得动点![]() 的轨迹方程;(2)由题意,可知直线
的轨迹方程;(2)由题意,可知直线![]() 的斜率为0时,不符合题意,当直线
的斜率为0时,不符合题意,当直线![]() 的斜率不为0时,则设直线
的斜率不为0时,则设直线![]() 的方程为:
的方程为:![]() ,将
,将![]() 的方程与椭圆方程联立,利用韦达定理求出
的方程与椭圆方程联立,利用韦达定理求出![]() ,
,![]() ,进而求出
,进而求出![]() ,可求出
,可求出![]() 的值,进而求出直线
的值,进而求出直线![]() 的方程.
的方程.
解:(1)设![]() 的坐标为
的坐标为![]() ,由题意可得
,由题意可得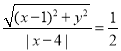 ,
,
整理可得:![]() ,
,
所以动点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]() ;
;
(2)当直线![]() 的斜率为0时,则直线
的斜率为0时,则直线![]() 为
为![]() ,
,
可得![]() ,
,![]() ,
,
则由题意![]() ,
,![]() ,则
,则![]() ;
;
当直线![]() 的斜率不为0时,则设直线
的斜率不为0时,则设直线![]() 的方程为:
的方程为:![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立直线![]() 与椭圆的方程:
与椭圆的方程: ,
,
整理可得![]() ,
,
则![]() ,
,![]() ,
,
所以![]() ,
,![]() 到
到![]() 的距离之差为:
的距离之差为:
![]()
![]()
![]() ,
,
由题意可得![]() ,整理可得:
,整理可得:![]() ,
,
解得:![]() ,即
,即![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.

练习册系列答案
相关题目
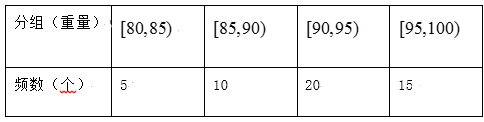
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: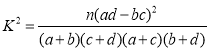 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%