题目内容
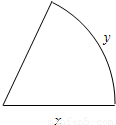
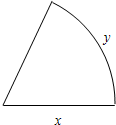 如图,设扇形的半径为x,弧长为y.
如图,设扇形的半径为x,弧长为y.(1)当该扇形的面积为常数S时,问半径x是多少时扇形的周长最小?并求出最小值;
(2)当该扇形的周长为常数P时,问半径x是多少时扇形的面积最大?并求出最大值.
分析:(1)先表示出S=
xy,然后表示出周长Z=2x+y,最后由均值不等式求的答案.
(2)先表示出2x+y=P,然后T=
xy,利用均值不等式求出结果.
| 1 |
| 2 |
(2)先表示出2x+y=P,然后T=
| 1 |
| 2 |
解答:解:(1)由题意得S=
xy,即xy=2S.(2分)
设扇形的周长为Z,则Z=2x+y≥2
=4
,(5分)
当且仅当2x=y,即x=
,y=2
时,Z可以取到最小值,最小值为4
.(7分)
(2)由题意得2x+y=P.(9分)
设扇形的面积为T,则T=
xy=
(2x)y≤
(
)2=
,(12分)
当且仅当2x=y,即x=
,y=
时,T可以取到最大值,最大值为
.(14分)
| 1 |
| 2 |
设扇形的周长为Z,则Z=2x+y≥2
| 2xy |
| S |
当且仅当2x=y,即x=
| S |
| S |
| S |
(2)由题意得2x+y=P.(9分)
设扇形的面积为T,则T=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2x+y |
| 2 |
| P2 |
| 16 |
当且仅当2x=y,即x=
| P |
| 4 |
| P |
| 2 |
| P2 |
| 16 |
点评:此题考查了扇形的面积以及均值不等式的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
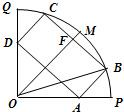 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ. 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?