题目内容
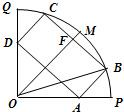 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.(I)将图书馆底面矩形ABCD的面积S表示成θ的函数.
(II)若R=45m,求当θ为何值时,矩形ABCD的面积S有最大值?其最大值是多少?(精确到0.01m2)
分析:(Ⅰ)要建立矩形面积模型,则只须表示出AB,BC即可,易知点M为
的中点,则有OM⊥AD.设OM于BC的交点为F,则BC=2Rsinθ,.AB=OF-
AD=Rcosθ-Rsinθ.再用面积公式求解.
(Ⅱ)由(I)由θ∈(0,
),确定2θ+
∈(
,
).再利用正弦函数最值求解.
 |
| PQ |
| 1 |
| 2 |
(Ⅱ)由(I)由θ∈(0,
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
解答:解:(Ⅰ)由题意可知,点M为
的中点,所以OM⊥AD.
设OM于BC的交点为F,则BC=2Rsinθ,OF=Rcosθ.AB=OF-
AD=Rcosθ-Rsinθ.
所以S=AB•BC=2Rsinθ(Rcosθ-Rsinθ)=R2(2sinθcosθ-2sin2θ)
=R2(sin2θ-1+cos2θ)=
R2sin(2θ+
)-R2,θ∈(0,
).
(Ⅱ)因为θ∈(0,
),则2θ+
∈(
,
).
所以当2θ+
=
,即θ=
时,S有最大值.
Smax=(
-1)R2=(
-1)×452=0.414×2025=838.35.
故当θ=
时,矩形ABCD的面积S有最大值838.35m2.
 |
| PQ |
设OM于BC的交点为F,则BC=2Rsinθ,OF=Rcosθ.AB=OF-
| 1 |
| 2 |
所以S=AB•BC=2Rsinθ(Rcosθ-Rsinθ)=R2(2sinθcosθ-2sin2θ)
=R2(sin2θ-1+cos2θ)=
| 2 |
| π |
| 4 |
| π |
| 4 |
(Ⅱ)因为θ∈(0,
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
所以当2θ+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
Smax=(
| 2 |
| 2 |
故当θ=
| π |
| 8 |
点评:本题主要考查应用题建模和解模问题,关键是明确关键词,关键句,建立模型的同时,也要明确条件.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ. 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?
 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径 ,
, ,
,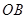 与
与 之间的夹角为
之间的夹角为 .
.
 的面积
的面积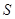 表示成
表示成