题目内容
15.已知正方形ABCD的外接圆的圆心O为坐标原点,直线AB的方程为x+2y-5=0.(Ⅰ)求直线AD的方程及圆O的方程;
(Ⅱ)是否存在两个点M和N,使得圆O上任意一点P到点M的距离与到点N的距离之比为$\frac{1}{2}$?如果存在,写出两点的坐标,并证明你的结论;如果不存在,请说明理由.
分析 (Ⅰ)由点到直线距离公式可求得直线AB到原点距离,继而可得正方形边长,然后勾股定理可得外接圆半径,然后求解外接圆方程,设出AD的方程,然后求解直线AD的方程.
(Ⅱ)结合圆的对称性,不妨设M、N在x轴上,利用条件列出P的方程,与第一问的结果比较,得到方程组,即可求解是否存在M、N.
解答 解:(Ⅰ)正方形ABCD的外接圆的圆心O为坐标原点,直线AB的方程为x+2y-5=0.
圆心到直线的距离为:$\frac{5}{\sqrt{1+{2}^{2}}}$=$\sqrt{5}$,圆的半径为:$\sqrt{10}$,所求圆的方程为:x2+y2=10,
直线AB的斜率为:-$\frac{1}{2}$,所以AD的斜率为:2,
则AD的方程为:y=2x+b,$\frac{\left|b\right|}{\sqrt{1+{2}^{2}}}$=$\sqrt{5}$,解得b=±5,
所求AB 的方程为:y=2x$±\sqrt{5}$.
(Ⅱ)圆的对称性可知,不妨设M(a,0),N(c,0).P(x,y)
由题意圆O上任意一点P到点M的距离与到点N的距离之比为$\frac{1}{2}$,可得:$\frac{(x-a)^{2}+{y}^{2}}{({x-c)}^{2}+{y}^{2}}=\frac{1}{4}$,
化简可得3x2+3y2-(8a-2c)x=c2-4a2.就是x2+y2=10,
可得8a-2c=0并且$\frac{{c}^{2}-4{a}^{2}}{3}=10$,解得a=$\frac{\sqrt{10}}{2}$,c=$\sqrt{10}$,或a=-$\frac{\sqrt{10}}{2}$,c=-$\sqrt{10}$.
∴存在两个点M和N.
点评 本题考查圆的方程的综合应用,直线与圆的位置关系,考查分析问题解决问题的能力.

 阅读快车系列答案
阅读快车系列答案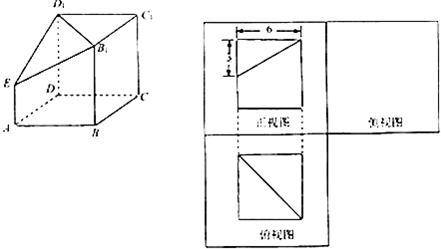 下列三个图中,左边是一个正方体截去一个角后所得的多面体的直观图,右边两个是正视图和俯视图.
下列三个图中,左边是一个正方体截去一个角后所得的多面体的直观图,右边两个是正视图和俯视图.