题目内容
5．设抛物线y2=4x上一点P到直线x=-3的距离为5，则点P到该抛物线焦点的距离是3．分析 抛物线y2=4x上一点P到直线x=-3的距离为5，可得：点P到抛物线的准线x=-1的距离为3，即可得出P到该抛物线焦点的距离．
解答 解：∵抛物线y2=4x上一点P到直线x=-3的距离为5，
∴点P到抛物线的准线x=-1的距离为3，
由抛物线的定义可得：点P到该抛物线焦点的距离是3．
故答案为：3．
点评 本题考查了抛物线的定义标准方程及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
20．已知直线m，l，平面α，β，且m⊥α，l?β，给出下列命题：
①若α∥β，则m⊥l； ②若α⊥β，则m∥l； ③若m⊥l，则α⊥β；④若m∥l，则α⊥β．
其中正确的命题的个数是（ ）
①若α∥β，则m⊥l； ②若α⊥β，则m∥l； ③若m⊥l，则α⊥β；④若m∥l，则α⊥β．
其中正确的命题的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
1．数学家欧拉在1765年提出定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后人称之为三角形的欧拉线．已知△ABC的顶点A（2，0），B（0，4），且AC=BC，则△ABC的欧拉线的方程为（ ）
| A． | x+2y+3=0 | B． | 2x+y+3=0 | C． | x-2y+3=0 | D． | 2x-y+3=0 |
10．抛物线y2=16x的焦点坐标为（ ）
| A． | （0，4） | B． | （0，-4） | C． | （4，0） | D． | （-4，0） |
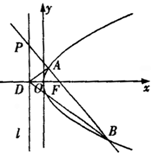如图，已知点F为抛物线C：y2=4x的焦点，点P是其准线l上的动点，直线PF交抛物线C于A、B两点．若点P的纵坐标为m（m≠0），点D为准线l与x轴的交点，则△DAB的面积S的取值范围为（4，+∞）．