题目内容
锐角
中，
、
、
分别为的三边
、
、
所对的角,
, 
,
．
（1）求角；
（2）求的面积
．
（1）
（2）
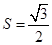
解析试题分析：解：（1）因为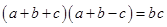
，所以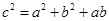
由余弦定理可得，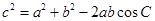
比较得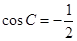
，所以
（2）
由正弦定理可得，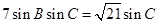
，
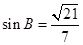由正弦定理可得，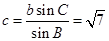
，又由余弦定理可得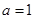
故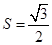
考点：正弦定理，余弦定理
点评：解决的关键是根据余弦定理和正弦定理来得到角和边的求解，从而求解三角形的面积，属于基础题。
练习册系列答案
相关题目
题目内容
锐角中，、、分别为的三边、、所对的角,, ,．
（1）求角；
（2）求的面积．
（1）（2）
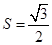
解析试题分析：解：（1）因为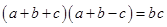，所以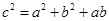
由余弦定理可得，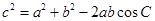
比较得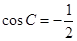，所以
（2）
由正弦定理可得，，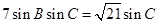
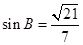由正弦定理可得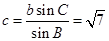，，又由余弦定理可得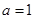
故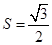
考点：正弦定理，余弦定理
点评：解决的关键是根据余弦定理和正弦定理来得到角和边的求解，从而求解三角形的面积，属于基础题。
的顶点与原点重合，始边与
轴非负半轴重合而终边经过点
．
的值；（2）求
的值．
在
的解的个数.
上的函数y＝f(x)的图象关于直线x＝－
对称，当x∈
时，函数f(x)＝Asin(ωx＋φ) 
的图象如图所示．
的解．
若角
的图象按向量
平移后,得到一个函数g(x)的图象，求g(x)的解析式. 
．
，求
的最大值及此时相应的
的值；
、b、c分别为角A、B、C的对边，若
，b =l，
，求
拟合（
，单位为小时,
表示气温，单位为摄氏度，
，
），
，函数
．
的最大值，并写出相应
的取值集合；
，且
，求
的值．
，其中向量
, (
R).
的最小正周期和最小值；
、
、
，若
，a=2
，
，求边长
的值.