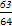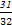题目内容
某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有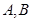 两个定点投篮位置,在
两个定点投篮位置,在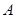 点投中一球得2分,在
点投中一球得2分,在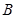 点投中一球得3分。某规则是:按先
点投中一球得3分。某规则是:按先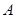 后
后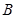 再
再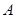 的顺序投篮,教师甲在
的顺序投篮,教师甲在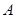 和
和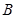 点投中的概率分别是
点投中的概率分别是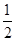 和
和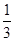 ,且在
,且在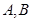 两点投中与否相互独立。
两点投中与否相互独立。
(1)若教师甲投篮三次,试求他投篮得分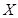 的分布列和数学期望;
的分布列和数学期望;
(2)若教师乙与教师甲在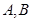 投中的概率相同,两人按规则各投三次,求甲胜乙的概率。
投中的概率相同,两人按规则各投三次,求甲胜乙的概率。
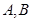 两个定点投篮位置,在
两个定点投篮位置,在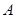 点投中一球得2分,在
点投中一球得2分,在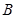 点投中一球得3分。某规则是:按先
点投中一球得3分。某规则是:按先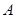 后
后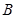 再
再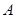 的顺序投篮,教师甲在
的顺序投篮,教师甲在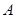 和
和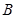 点投中的概率分别是
点投中的概率分别是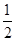 和
和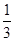 ,且在
,且在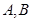 两点投中与否相互独立。
两点投中与否相互独立。(1)若教师甲投篮三次,试求他投篮得分
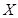 的分布列和数学期望;
的分布列和数学期望;(2)若教师乙与教师甲在
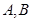 投中的概率相同,两人按规则各投三次,求甲胜乙的概率。
投中的概率相同,两人按规则各投三次,求甲胜乙的概率。(1)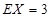 ;(2)
;(2)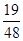
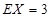 ;(2)
;(2)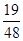
试题分析:(1)根据题意知X的可能取值为0,2,3,4,5,7,根据相互独立同时发生的概率公式可求其概率,从而可求其分布列,根据期望公式可求其期望值。(2)教师甲胜乙包括以下几种情况:甲得2分乙得0分;甲得3分乙的2分或0分;甲得4分乙得0分或2分或3分;甲得5分乙得0分或2分或3分或4分;甲得7分乙得0分或2分或3分或4分或5分。按照相互独立及互斥事件概率求其概率即可。
试题解析:解答:设“教师甲在
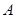 点投中”的事件为
点投中”的事件为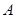 ,“教师甲在
,“教师甲在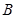 点投中”的事件为
点投中”的事件为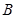 .
.(1)根据题意知X的可能取值为0,2,3,4,5,7
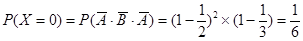 ,
,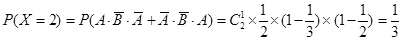
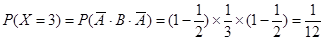
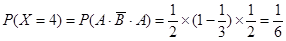

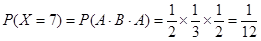 6分
6分所以X的分布列是:
]
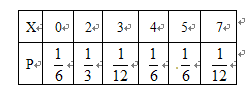
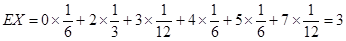 8分
8分(2)教师甲胜乙包括:甲得2分、3分、4分、5分、7分五种情形.
这五种情形之间彼此互斥,因此,所求事件的概率
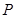 为:
为: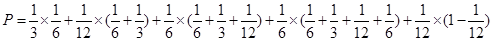
 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
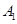 ,
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。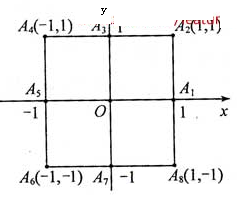
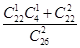 等于________(用概率的式子表示).
等于________(用概率的式子表示).



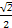 ),则P(-2≤X≤5.5)=( )
),则P(-2≤X≤5.5)=( )