题目内容
14.某人在塔的正东沿着南偏西60°的方向前进40米后,望见塔在东北方向,若沿途测得塔顶的最大仰角为30°,求塔高.分析 在△BCD中,由正弦定理得BD=$\frac{40sin30°}{sin135°}$=20$\sqrt{2}$,在Rt△BED中,由题意可求∠BDE,而由BE=DBsin∠BDE可求BE,然后由AB=BEtan∠AEB可求AB即塔高.
解答 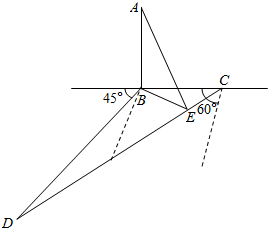 解:在△BCD中,CD=40,∠BCD=30°,∠DBC=135°
解:在△BCD中,CD=40,∠BCD=30°,∠DBC=135°
由正弦定理得BD=$\frac{40sin30°}{sin135°}$=20$\sqrt{2}$…(5分)
由题意BE⊥CD∴在Rt△BED中,∠BDE=180°-135°-30°=15°
∴BE=DBsin15°=20$\sqrt{2}$•$\frac{\sqrt{6}-\sqrt{2}}{4}$=10$\sqrt{3}$-10…(9分)
在Rt△ABE中,∠AEB=30°
∴AB=BEtan30°=$\frac{10}{3}$(3-$\sqrt{3}$)…(11分)
故所求的塔高为$\frac{10}{3}$(3-$\sqrt{3}$)米.
点评 本题主要考查了实际问题的求解,解题的关键是要把实际问题转化为数学问题,然后结合合适的公式进行求解.

练习册系列答案
相关题目
19.记曲线y=$\sqrt{1-(x-1)^{2}}$与x轴所围成的区域为D,若曲线y=ax(x-2)(a<0)把D的面积均分为两等份,则a的值为( )
| A. | -$\frac{3}{8}$ | B. | -$\frac{3π}{16}$ | C. | -$\frac{3π}{8}$ | D. | -$\frac{π}{16}$ |