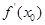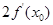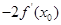题目内容
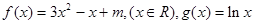
(1)若函数 f(x)与 g(x)的图像在 x=x0处的切线平行,求x0的值
(2)当曲线
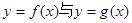 有公共切线时,求函数
有公共切线时,求函数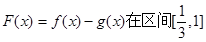 上的最值
上的最值(3)求证:当m>-2时,对一切正整数n,不等式f(x)> g(x)在区间 [n,n+1]上恒成立
(1)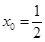 ;
;
(2)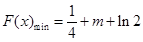 ,
,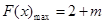 ;
;
(3)见解析
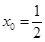 ;
;(2)
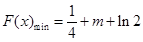 ,
,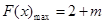 ;
;(3)见解析
本试题主要考查了导数在研究函数中的运用。
(1)因为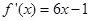 ,
,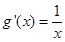 ,则
,则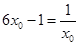 ,即
,即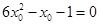 ,从而得到点的坐标。
,从而得到点的坐标。
(2)由(1)得切点横坐标为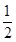 ,∴
,∴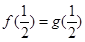 ,∴
,∴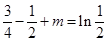 ∴
∴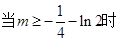 ,
,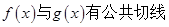 ,然后构造函数
,然后构造函数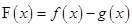 ,利用导数来排尿的尼姑单调性得到最值证明不等式成立。
,利用导数来排尿的尼姑单调性得到最值证明不等式成立。
解:(1)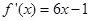 ,
,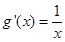 ,则
,则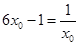 ,即
,即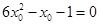
解得,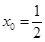 或
或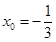 (舍去)
(舍去)
(2)由(1)得切点横坐标为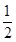 ,∴
,∴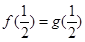 ,∴
,∴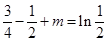
∴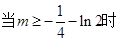 ,
,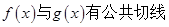 ,
,
令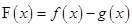 ,
,
则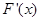
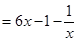
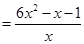
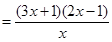
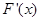 与
与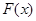 的变化如下表
的变化如下表
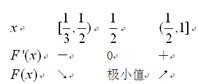
又∵ ,
,
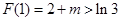 ,
,
∴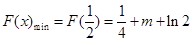 ,
,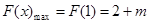
(3)函数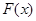 =
=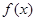 -
-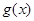 在区间
在区间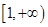 上是增函数,且
上是增函数,且
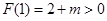 ,∴当x≥1时,
,∴当x≥1时,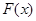 ≥
≥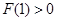
即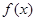 >
>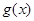 在区间[1,+∞)上恒成立
在区间[1,+∞)上恒成立
∴原命题成立.
(1)因为
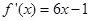 ,
,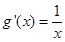 ,则
,则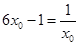 ,即
,即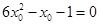 ,从而得到点的坐标。
,从而得到点的坐标。(2)由(1)得切点横坐标为
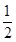 ,∴
,∴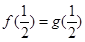 ,∴
,∴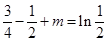 ∴
∴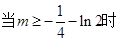 ,
,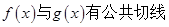 ,然后构造函数
,然后构造函数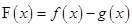 ,利用导数来排尿的尼姑单调性得到最值证明不等式成立。
,利用导数来排尿的尼姑单调性得到最值证明不等式成立。解:(1)
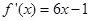 ,
,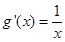 ,则
,则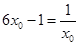 ,即
,即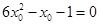
解得,
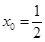 或
或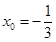 (舍去)
(舍去)(2)由(1)得切点横坐标为
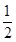 ,∴
,∴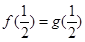 ,∴
,∴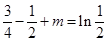
∴
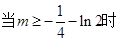 ,
,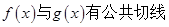 ,
,令
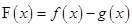 ,
,则
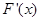
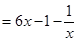
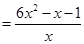
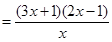
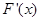 与
与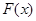 的变化如下表
的变化如下表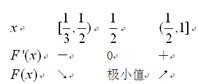
又∵
 ,
,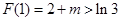 ,
,∴
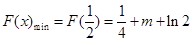 ,
,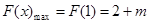
(3)函数
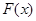 =
=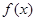 -
-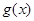 在区间
在区间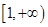 上是增函数,且
上是增函数,且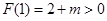 ,∴当x≥1时,
,∴当x≥1时,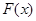 ≥
≥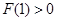
即
 >
> 在区间[1,+∞)上恒成立
在区间[1,+∞)上恒成立∴原命题成立.

练习册系列答案
相关题目
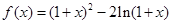 .
.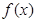 的单调区间;
的单调区间;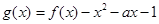 在区间
在区间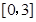 上的最小值.
上的最小值. ,点P的坐标为 ( )
,点P的坐标为 ( )



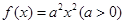 ,
, 。
。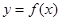 图象上的点到直线
图象上的点到直线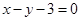 距离的最小值是
距离的最小值是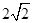 ,求
,求 的值。
的值。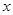 的不等式
的不等式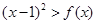 的解集中的整数恰好有3个,求实数
的解集中的整数恰好有3个,求实数 上一点P处的切线与直线
上一点P处的切线与直线 平行,则点P的坐标为_______
平行,则点P的坐标为_______  在点
在点 处的切线的斜率为
处的切线的斜率为


 的导数为( )
的导数为( )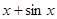
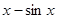
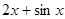
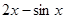
 ,f(1)=-1,则此函数为( )
,f(1)=-1,则此函数为( )

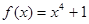

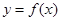 在区间
在区间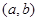 内可导,且
内可导,且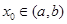 则
则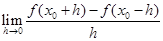 的值为
的值为