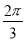题目内容
5.设函数f(x)=$\frac{{x}^{2}}{x-2}$,求f(0),f(1),f(-x+1).分析 分别将x=0,x=1,x=-x+1代入函数的解析式求出即可.
解答 解:∵函数f(x)=$\frac{{x}^{2}}{x-2}$,
∴f(0)=0,
f(1)=-1,
f(-x+1)=$\frac{{(-x+1)}^{2}}{-x+1-2}$=-$\frac{{(x-1)}^{2}}{x+1}$.
点评 本题考查了求函数值问题,是一道基础题.

练习册系列答案
相关题目
15.设a=30.3,b=50.2,c=60.1,则a,b,c的大小关系是( )
| A. | c<b<a | B. | a<c<b | C. | a<b<c | D. | c<a<b |
2.己知f(x)=2sin(x+$\frac{π}{3}$)(x∈R),函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
10.下列图象表示的函数中具有奇偶性的是( )
| A. |  | B. |  | C. |  | D. | 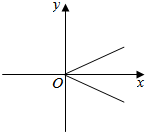 |

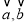 ,满足
,满足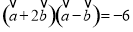 ,且
,且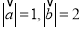 ,则
,则 与
与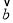 的夹角为( )
的夹角为( )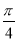 B.
B.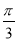 C.
C.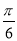 D.
D.