题目内容
已知椭圆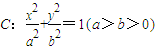 的离心率
的离心率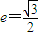 ,且过点
,且过点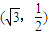 .
.(1)求椭圆C的标准方程;
(2)垂直于坐标轴的直线l与椭圆C相交于A、B两点,若以AB为直径的圆D经过坐标原点.证明:圆D的半径为定值.
【答案】分析:(1)根据椭圆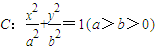 的离心率
的离心率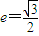 ,可得a2=4b2,利用椭圆过点
,可得a2=4b2,利用椭圆过点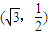 ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程;
(2)设A(x1,y1),B(x2,y2),分类讨论:①当直线AB斜率不存在时,由椭圆的对称性可知x1=x2,y1=-y2,从而可求原点O到直线的距离;②当直线AB斜率为0时,由椭圆的对称性可知x1=-x2,y1=y2,可求原点O到直线的距离,由此可知圆D的半径为定值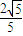 .
.
解答:(1)解:∵椭圆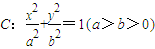 的离心率
的离心率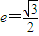
∴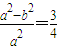 ,∴a2=4b2
,∴a2=4b2
∴椭圆C的方程为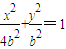
∵椭圆过点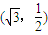
∴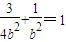
∴b2=1,a2=4
∴椭圆C的标准方程为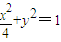
(2)证明:设A(x1,y1),B(x2,y2)
①当直线AB斜率不存在时,由椭圆的对称性可知x1=x2,y1=-y2,
∵以AB为直径的圆D经过坐标原点,∴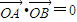
∴x1x2+y1y2=0,∴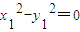
∵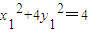 ,∴
,∴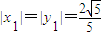
∴原点O到直线的距离为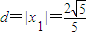
②当直线AB斜率为0时,由椭圆的对称性可知x1=-x2,y1=y2,
∵以AB为直径的圆D经过坐标原点,∴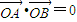
∴x1x2+y1y2=0,∴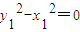
∵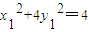 ,∴
,∴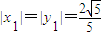
∴原点O到直线的距离为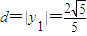
综上知,圆D的半径为定值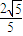 .
.
点评:本题考查椭圆的标准方程,考查圆与椭圆的综合,正确运用椭圆的性质是解题的关键.
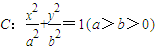 的离心率
的离心率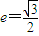 ,可得a2=4b2,利用椭圆过点
,可得a2=4b2,利用椭圆过点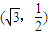 ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程;(2)设A(x1,y1),B(x2,y2),分类讨论:①当直线AB斜率不存在时,由椭圆的对称性可知x1=x2,y1=-y2,从而可求原点O到直线的距离;②当直线AB斜率为0时,由椭圆的对称性可知x1=-x2,y1=y2,可求原点O到直线的距离,由此可知圆D的半径为定值
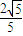 .
.解答:(1)解:∵椭圆
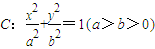 的离心率
的离心率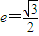
∴
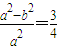 ,∴a2=4b2
,∴a2=4b2∴椭圆C的方程为
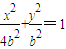
∵椭圆过点
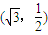
∴
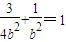
∴b2=1,a2=4
∴椭圆C的标准方程为
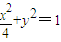
(2)证明:设A(x1,y1),B(x2,y2)
①当直线AB斜率不存在时,由椭圆的对称性可知x1=x2,y1=-y2,
∵以AB为直径的圆D经过坐标原点,∴
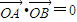
∴x1x2+y1y2=0,∴
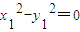
∵
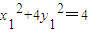 ,∴
,∴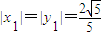
∴原点O到直线的距离为
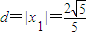
②当直线AB斜率为0时,由椭圆的对称性可知x1=-x2,y1=y2,
∵以AB为直径的圆D经过坐标原点,∴
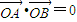
∴x1x2+y1y2=0,∴
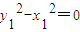
∵
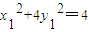 ,∴
,∴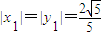
∴原点O到直线的距离为
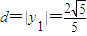
综上知,圆D的半径为定值
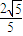 .
.点评:本题考查椭圆的标准方程,考查圆与椭圆的综合,正确运用椭圆的性质是解题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 的离心率
的离心率 ,且右焦点F到左准线的距离为3.
,且右焦点F到左准线的距离为3. ,求p的最大值.
,求p的最大值.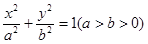 的离心率为
的离心率为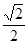 ,且过点
,且过点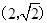 .
.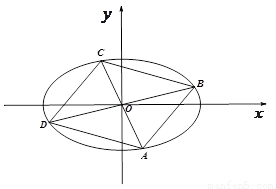
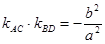 ,
,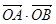 的最值.
的最值.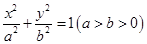 的离心率
的离心率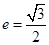 ,且短半轴
,且短半轴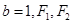 为其左右焦点,
为其左右焦点,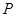 是椭圆上动点.
是椭圆上动点.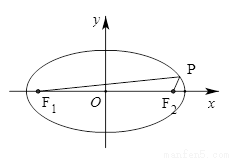
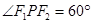 时,求
时,求 面积;
面积;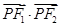 取值范围.
取值范围.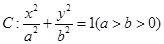 的离心率
的离心率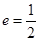 ,且椭圆过点
,且椭圆过点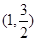 .
.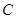 的方程;
的方程;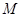 为椭圆
为椭圆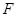 为椭圆的右焦点,以
为椭圆的右焦点,以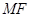 长为半径作圆
长为半径作圆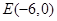 作圆
作圆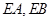 ,(
,(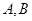 为切点),求点
为切点),求点 的面积最大.]
的面积最大.]