题目内容
(本小题满分13分)
已知椭圆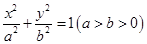 的离心率
的离心率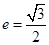 ,且短半轴
,且短半轴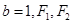 为其左右焦点,
为其左右焦点,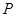 是椭圆上动点.
是椭圆上动点.
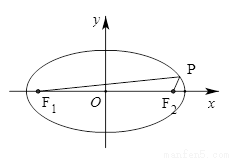
(Ⅰ)求椭圆方程;
(Ⅱ)当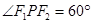 时,求
时,求 面积;
面积;
(Ⅲ)求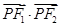 取值范围.
取值范围.
【答案】
(Ⅰ)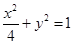 ;(Ⅱ)
;(Ⅱ)  ;(Ⅲ)
;(Ⅲ) 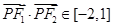
【解析】
试题分析:(Ⅰ)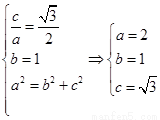
∴椭圆方程为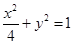 4分
4分
(Ⅱ)设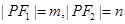 ,
,
∵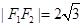 ,在
,在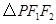 中,由余弦定理得:
中,由余弦定理得:
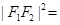
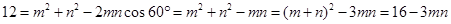
∴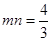 7分
7分
∴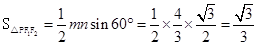 9分
9分
(Ⅲ)设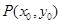 ,则
,则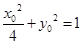 ,即
,即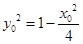
∵ ,∴
,∴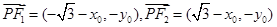
∴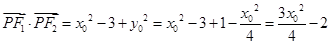 11分
11分
∵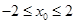 ,∴
,∴
故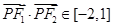 13分
13分
考点:本题考查了椭圆方程、椭圆性质,解三角形,向量的数量积.
点评:解答时注意以下的转化:⑴若直线与圆锥曲线有两个交点,对待交点坐标是“设而不求”的原则,要注意应用韦达定理处理这类问题; ⑵平面向量与解析几何综合题,遵循的是平面向量坐标化,应用的是平面向量坐标运算法则还有两向量平行、垂直来解决问题,这就要求同学们在基本概念、基本方法、基本能力上下功夫.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和