题目内容
已知椭圆 的离心率
的离心率 ,且右焦点F到左准线的距离为3.
,且右焦点F到左准线的距离为3.(1)求椭圆C的方程;
(2)已知B为椭圆C在y轴的左测上一点,线段BF与抛物线y2=2px(p>0)交于A,且满足
 ,求p的最大值.
,求p的最大值.
【答案】分析:(1)由已知离心率及点F到准线的距离,列方程即可得a、b、c的值;(2)设B(x,y),A(xA,yA),利用向量相等的意义得两点坐标间的关系,分别代入椭圆和抛物线方程即可得p关于
x的函数,利用换元法求值域即可
解答:解:(1)∵ 的离心率
的离心率 ,∴
,∴ .①
.①
而右焦点到左准线之距 .②
.②
又a2=b2+c2 ③
由①②③解之得 ,b=1.
,b=1.
从而所求椭圆方程为 .
.
(2)椭圆的右焦点为F(1,0),点B在椭圆 上,
上,
设B(x,y),其中 ,设A(xA,yA)
,设A(xA,yA)
由 ,得(x-xA,y-yA)=2(xA-1,yA)
,得(x-xA,y-yA)=2(xA-1,yA)
∴ .
.
由点A在抛物线y2=2px上,得 .
.
又 ,
,
∴ .
.
令t=x+2,则 ,
,
即 .
.
∵ .∴
.∴ (当且仅当
(当且仅当 时取“=”).
时取“=”).
∴ .
.
又当 时,
时, 为椭圆在y轴左侧上的点.
为椭圆在y轴左侧上的点.
故p的最大值为 .
.
点评:本题考查了椭圆的标准方程和几何性质,抛物线的标准方程,利用函数求最值的思想方法,向量在解析几何中的应用
x的函数,利用换元法求值域即可
解答:解:(1)∵
 的离心率
的离心率 ,∴
,∴ .①
.①而右焦点到左准线之距
 .②
.②又a2=b2+c2 ③
由①②③解之得
 ,b=1.
,b=1.从而所求椭圆方程为
 .
.(2)椭圆的右焦点为F(1,0),点B在椭圆
 上,
上,设B(x,y),其中
 ,设A(xA,yA)
,设A(xA,yA)由
 ,得(x-xA,y-yA)=2(xA-1,yA)
,得(x-xA,y-yA)=2(xA-1,yA)∴
 .
.由点A在抛物线y2=2px上,得
 .
.又
 ,
,∴
 .
.令t=x+2,则
 ,
,即
 .
.∵
 .∴
.∴ (当且仅当
(当且仅当 时取“=”).
时取“=”).∴
 .
.又当
 时,
时, 为椭圆在y轴左侧上的点.
为椭圆在y轴左侧上的点.故p的最大值为
 .
.点评:本题考查了椭圆的标准方程和几何性质,抛物线的标准方程,利用函数求最值的思想方法,向量在解析几何中的应用

练习册系列答案
相关题目
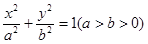 的离心率为
的离心率为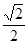 ,且过点
,且过点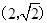 .
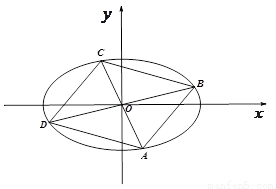
.
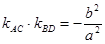 ,
,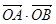 的最值.
的最值.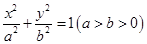 的离心率
的离心率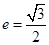 ,且短半轴
,且短半轴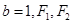 为其左右焦点,
为其左右焦点,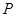 是椭圆上动点.
是椭圆上动点.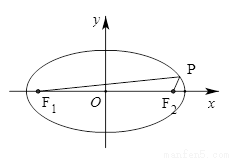
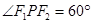 时,求
时,求 面积;
面积;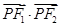 取值范围.
取值范围.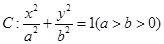 的离心率
的离心率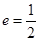 ,且椭圆过点
,且椭圆过点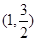 .
.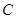 的方程;
的方程;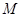 为椭圆
为椭圆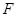 为椭圆的右焦点,以
为椭圆的右焦点,以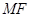 长为半径作圆
长为半径作圆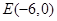 作圆
作圆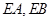 ,(
,(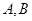 为切点),求点
为切点),求点 的面积最大.]
的面积最大.]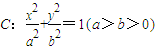 的离心率
的离心率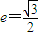 ,且过点
,且过点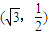 .
.