题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)当![]() 时,记函数
时,记函数![]() 的所有单调递增区间的长度为
的所有单调递增区间的长度为![]() ,所有单调递减区间的长度为
,所有单调递减区间的长度为![]() ,证明:
,证明:![]() .(注:区间长度指该区间在
.(注:区间长度指该区间在![]() 轴上所占位置的长度,与区间的开闭无关.)
轴上所占位置的长度,与区间的开闭无关.)
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)首先求函数的导数,然后判断函数的单调性,最后求最值;
(2)根据(1)首先求函数![]() 的零点,从而去掉
的零点,从而去掉![]() 的绝对值,分段求函数
的绝对值,分段求函数![]() 的单调区间,最后再比较单调区间的长度.
的单调区间,最后再比较单调区间的长度.
解(1)因为![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,
所以![]() .
.
(2)由(1)可知,![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增
单调递增
又![]() ,
,![]() ,
,![]()
所以存在![]() ,使得
,使得![]() ,
,
则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以,
记![]() ,
,![]()
当![]() 时,
时,![]() ,所以
,所以
![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
当![]() 或
或![]() 时,
时,![]()
当![]() 时
时![]() 即
即![]() 在
在![]() 单调递增.
单调递增.
因为![]() ,所以
,所以![]()
则当![]() 时,令
时,令![]() ,有
,有![]()
所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减
单调递减
综上,![]() 在
在![]() 与
与![]() 单调递减,在
单调递减,在![]() 与
与![]() 单调递增.
单调递增.
所以![]() ,
,![]() 又
又![]()
所以![]() ,即
,即![]()

 名校课堂系列答案
名校课堂系列答案【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
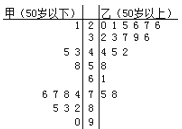
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了 30 名同学,得到如下的 ![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用学习成绩优秀的 12 名同学中,随机抽取 2 名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中倍抽取的 5 名同学,再随机抽取 3 名同学,试求抽取 3 名同学中恰有 2 名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

