题目内容
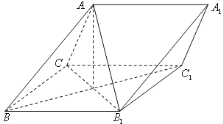
【题目】已知四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() 底面
底面![]() 且
且![]()
![]() 是
是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求![]() 与
与![]() 夹角的余弦值;
夹角的余弦值;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
建立空间直角坐标系,求出![]() 的坐标,
的坐标,
(1)通过证明![]() ,利用
,利用![]() ,即可证明结论成立;
,即可证明结论成立;
(2)求出![]() 与
与![]() 的方向向量,由
的方向向量,由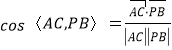 ,即可求出结果;
,即可求出结果;
(3)在![]() 上取一点
上取一点![]() ,则存在
,则存在![]() ,使
,使![]() ,求出
,求出![]() ,再说明
,再说明![]() 为所求二面角的平面角,利用向量夹角公式即可求出结果.
为所求二面角的平面角,利用向量夹角公式即可求出结果.
以A为坐标原点,建立空间直角坐标系,
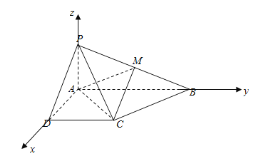
则![]()
(1)证明:因为![]()
所以![]() ,所以
,所以![]() .
.
由题设知![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为![]() ,
,![]() ,
,
所以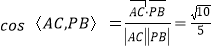
故![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
(3)在![]() 上取一点
上取一点![]() ,则存在
,则存在![]() ,使
,使![]() ,又
,又
![]()
所以![]() ,
,
要使![]() ,只需
,只需![]() ,即
,即![]() ,解得
,解得![]() ,可知
,可知![]() 当时,N点的坐标为
当时,N点的坐标为![]() ,能使
,能使![]() ,此时
,此时![]() ,有
,有![]() ,
,
由![]() 得
得![]() ,
,
所以![]() 为所求二面角的平面角.
为所求二面角的平面角.
所以![]() ,
,
所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

【题目】某地公共电汽车和地铁按照里程分段计价,具体如下表:
乘公共电汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
乘坐地铁方案 | 6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含) |
已知在一号线地铁上,任意一站到![]() 站的票价不超过5元,现从那些只乘坐一号线地铁,且在
站的票价不超过5元,现从那些只乘坐一号线地铁,且在![]() 站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
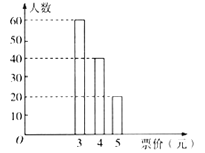
(Ⅰ)如果从那些只乘坐一号线地铁,且在![]() 站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
(Ⅱ)已知选出的120人中有6名学生,且这6名学生中票价为3、4、5元的人数分别为3,2,1人,现从这6人中随机选出2人,求这2人的票价和恰好为8元的概率;
(Ⅲ)小李乘坐一号线地铁从![]() 地到
地到![]() 站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为
站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为![]() 公里,试写出
公里,试写出![]() 的取值范围.
的取值范围.