题目内容
【题目】已知椭圆C: ![]() =1的离心率为
=1的离心率为 ![]() ,焦距为2,右焦点为F,过点F的直线交椭圆于A、B两点.
,焦距为2,右焦点为F,过点F的直线交椭圆于A、B两点.
(1)求椭圆C的方程;
(2)在x轴上是否存在定点M,使得 ![]() 为定值?若存在,求出定值和定点坐标;若不存在,请说明理由.
为定值?若存在,求出定值和定点坐标;若不存在,请说明理由.
【答案】
(1)解:由题意可得2c=2,e= ![]() =
= ![]() ,
,
可得c=1,a= ![]() ,b=
,b= ![]() =1,
=1,
即有椭圆的方程为 ![]() +y2=1
+y2=1
(2)解:在x轴上假设存在定点M(m,0),使得 ![]() 为定值.
为定值.
若直线的斜率存在,设AB的斜率为k,F(1,0),
由y=k(x﹣1)代入椭圆方程x2+2y2=2,
可得(1+2k2)x2﹣4k2x+2k2﹣2=0,
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
y1y2=k2(x1﹣1)(x2﹣1)=k2[x1x2+1﹣(x1+x2)]
=k2( ![]() +1﹣
+1﹣ ![]() )=﹣
)=﹣ ![]() ,
,
则 ![]() =(x1﹣m)(x2﹣m)+y1y2=x1x2+m2﹣m(x1+x2)+y1y2
=(x1﹣m)(x2﹣m)+y1y2=x1x2+m2﹣m(x1+x2)+y1y2
= ![]() +m2﹣m
+m2﹣m ![]() ﹣
﹣ ![]() =
= 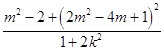 ,
,
欲使得 ![]() 为定值,则2m2﹣4m+1=2(m2﹣2),
为定值,则2m2﹣4m+1=2(m2﹣2),
解得m= ![]() ,
,
此时 ![]() =
= ![]() ﹣2=﹣
﹣2=﹣ ![]() ;
;
当AB斜率不存在时,令x=1,代入椭圆方程,可得y=± ![]() ,
,
由M( ![]() ,0),可得
,0),可得 ![]() ﹣
﹣ ![]() ,符合题意.
,符合题意.
故在x轴上存在定点M( ![]() ,0),使得
,0),使得 ![]() 为定值﹣
为定值﹣ ![]()
【解析】(1)由题意可得c=1,运用离心率公式可得a= ![]() ,由a,b,c的关系可得b=1,进而得到椭圆方程;(2)在x轴上假设存在定点M(m,0),使得
,由a,b,c的关系可得b=1,进而得到椭圆方程;(2)在x轴上假设存在定点M(m,0),使得 ![]() 为定值.若直线的斜率存在,设AB的斜率为k,F(1,0),由y=k(x﹣1)代入椭圆方程,运用韦达定理和向量数量积的坐标表示,结合恒成立思想,即可得到定点和定值;检验直线AB的斜率不存在时,也成立.
为定值.若直线的斜率存在,设AB的斜率为k,F(1,0),由y=k(x﹣1)代入椭圆方程,运用韦达定理和向量数量积的坐标表示,结合恒成立思想,即可得到定点和定值;检验直线AB的斜率不存在时,也成立.

【题目】假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
2 | 3 | 4 | 5 | 6 | |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程![]() =bx+
=bx+![]() ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(参考数据:2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)