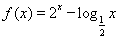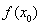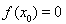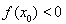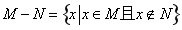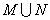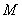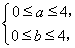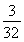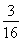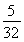题目内容
如图，已知椭圆的中心在坐标原点，焦点在x轴上，长轴长是短轴长的2倍，且经过点M(2,1)，平行于OM的直线l在y轴上的截距为m，直线l与椭圆相交于A，B两个不同点．
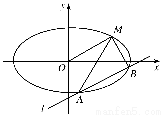
(1)求实数m的取值范围；
(2)证明：直线MA，MB与x轴围成的三角形是等腰三角形．
（1）(－2,0)∪(0,2)（2）见解析
【解析】(1)设椭圆方程为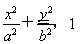
(a＞b＞0)，
由题意得
∴
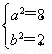
∴椭圆方程为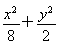
＝1.
由题意可得直线l的方程为y＝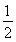
x＋m(m≠0)，
设A(x1，y1)，B(x2，y2)，
则点A，B的坐标是方程组
的两组解，
消去y得x2＋2mx＋2m2－4＝0.
∵Δ＝4m2－4(2m2－4)＞0，∴－2＜m＜2.
又∵m≠0，∴实数m的取值范围为(－2,0)∪(0,2)．
(2)证明：由题意可设直线MA，MB的斜率分别为k1，k2，
只需证明k1＋k2＝0即可，
由(1)得x2＋2mx＋2m2－4＝0，
∴x1＋x2＝－2m，x1x2＝2m2－4，
∵k1＋k2＝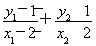
＝
＝
? ?＝
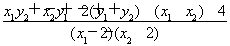
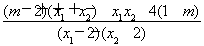＝0， ?
∴直线MA，MB与x轴围成的三角形是等腰三角形．
练习册系列答案
相关题目
