题目内容
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.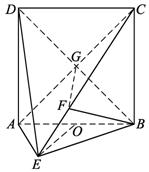
(1)求证:AE⊥平面BCE;
(2)求二面角B—AC—E的大小;
(3)求点D到平面ACE的距离.
(1)证明:∵BF⊥平面ACE,
∴BF⊥AE.
∵二面角D—AB—E为直二面角,且CB⊥AB,
∴CB⊥平面ABE.
∴CB⊥AE.
∴AE⊥平面BCE.
(2)解:连结BD交AC于点G,连结FG.
∵正方形ABCD的边长为2,
∴BG⊥AC,BG=![]() .
.
∵BF⊥平面ACE,
由三垂线定理的逆定理,得FG⊥AC.
∴∠BGF是二面角B—AC—E的平面角.
由(1)AE⊥平面BCE,
∴AE⊥EB.
又∵AE=EB,∴在等腰Rt△AEB中,BE=![]() .
.
又∵Rt△BCE中,
EC=![]() ,
,
BF=![]() ,∴Rt△BFG中,
,∴Rt△BFG中,
sin∠BGF=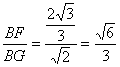 .
.
∴二面角B—AC—E等于arcsin![]() .
.
(3)解:过E作EO⊥AB交AB于点O,OE=1.
∵二面角D—AB—E为直二面角,
∴EO⊥平面ABCD.
设D到平面ACE的距离为h,
∵VD—ACE=VE—ACD,
∴![]() S△ACE·h=
S△ACE·h=![]() S△ACD·EO.
S△ACD·EO.
∵AE⊥平面BCE,
∴AE⊥EC.
∴h=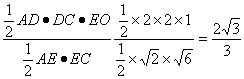
∴点D到平面ACE的距离为![]() .
.

练习册系列答案
相关题目
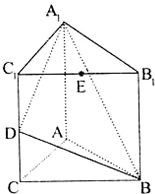 直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.
直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.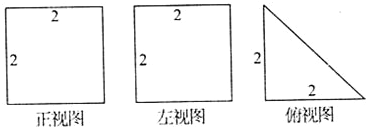
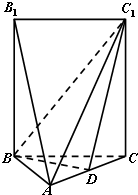 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.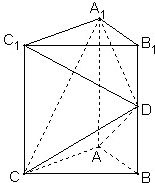 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点. 如图,直四棱柱A1B1C1D1-ABCD的高为3,底面是边长为4,且∠DAB=60°的菱形,O是AC与BD的交点,O1是A1C1与B1D1的交点.
如图,直四棱柱A1B1C1D1-ABCD的高为3,底面是边长为4,且∠DAB=60°的菱形,O是AC与BD的交点,O1是A1C1与B1D1的交点.