题目内容
若函数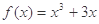
对任意的
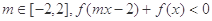恒成立，则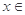
.
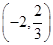
解析试题分析：由题意，
是奇函数且为单调递增函数，则
，由递增函数的性质有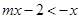
，所以原题等价于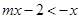在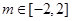
上恒成立，构造函数
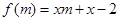，由题意有
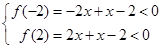，解得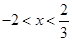
.解题思路：（1）根据给定的函数确定函数的性质，可以将
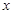的关系从中脱离出来，最好不能带入原函数；（2）当考查恒成立问题时，并且告知我们两个参数，如知道的是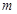
的范围，我们就以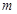为主元.
考点：1.函数的单调性和奇偶性；2.函数恒成立问题.
练习册系列答案
相关题目
题目内容
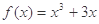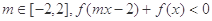若函数对任意的恒成立，则 .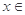
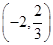
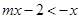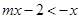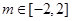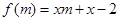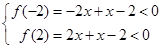解析试题分析：由题意，是奇函数且为单调递增函数，则，由递增函数的性质有，所以原题等价于在上恒成立，构造函数，由题意有，解得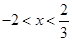.解题思路：（1）根据给定的函数确定函数的性质，可以将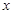的关系从中脱离出来，最好不能带入原函数；（2）当考查恒成立问题时，并且告知我们两个参数，如知道的是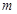的范围，我们就以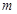为主元.
考点：1.函数的单调性和奇偶性；2.函数恒成立问题.
，定义域为
，则函数
的定义域为_______．
是定义在
上的奇函数，且当
时，
，若对任意
，不等式
恒成立，则实数
的取值范围是 ．
是
上的奇函数，
时，
，若对于任意
，都有
，则
的值为 .
上的奇函数
，当
时，
，那么，
.
，给出下列四个命题：
，
时，
只有一个实数根；
时，
是奇函数；
，
对称；
至多有两个零点.
的定义域是 ．
的取值范围是 ．
有 个不同的实数根