题目内容
10.若(1+ex)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),则-$\frac{{a}_{1}}{e}+\frac{{a}_{2}}{{e}^{2}}-\frac{{a}_{3}}{{e}^{3}}$+…+$\frac{{a}_{2014}}{{e}^{2014}}$=-1.分析 在(1+ex)2014=a0+a1x+a2x2+…+a2014x2014(x∈R)中,令x=-$\frac{1}{e}$,0,即可得出结论.
解答 解:在(1+ex)2014=a0+a1x+a2x2+…+a2014x2014(x∈R)中,
令x=-$\frac{1}{e}$,可得a0-$\frac{{a}_{1}}{e}+\frac{{a}_{2}}{{e}^{2}}-\frac{{a}_{3}}{{e}^{3}}$+…+$\frac{{a}_{2014}}{{e}^{2014}}$=0.
再令x=0可得a0=1,∴-$\frac{{a}_{1}}{e}+\frac{{a}_{2}}{{e}^{2}}-\frac{{a}_{3}}{{e}^{3}}$+…+$\frac{{a}_{2014}}{{e}^{2014}}$=-1.
故答案为:-1.
点评 本题考查二项式定理的应用,考查赋值法,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
19.从4个不同的独唱节目和2个不同的合唱节目中选出4个节目编排一个节目单,要求最后一个节目必须是合唱,则这个节目单的编排方法共有( )
| A. | 14种 | B. | 48种 | C. | 72种 | D. | 120种 |
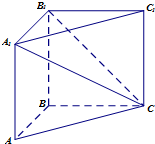 如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.
如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.