题目内容
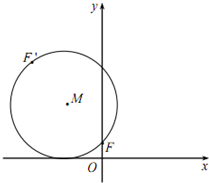 (2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
(2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.(1)求曲线C的方程;
(2)设A(x0,y0)是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P、Q.
①证明:直线PQ的斜率为定值;
②记曲线C位于P、Q两点之间的那一段为l.若点B在l上,且点B到直线PQ的距离最大,求点B的坐标.
分析:(1)设F′(x,y),则可得M(
,
),圆M的直径为|FF′|=
,利用动圆M与x轴相切,即可求得曲线C的方程;
(2)①确定A(x0,
),设P(x1,
),Q(x2,
),利用直线AP,AQ的倾斜角互补,可得它们的斜率互为相反数,从而可得直线PQ的斜率;
②由①可知,kPQ=-
,则若点B在曲线段L上,且点B到直线PQ的距离最大,曲线C在点B处的切线l∥PQ,设直线的方程,代入抛物线方程,利用判别式,即可求得结论.
| x |
| 2 |
| y+1 |
| 2 |
| x2+(y-1)2 |
(2)①确定A(x0,
| x02 |
| 4 |
| x12 |
| 4 |
| x22 |
| 4 |
②由①可知,kPQ=-
| x0 |
| 2 |
解答:(1)解:设F′(x,y),因为点F(1,0)在圆M上,且点F关于圆心M的对称点为F′,
所以M(
,
),…(1分)
且圆M的直径为|FF′|=
.…(2分)
由题意,动圆M与x轴相切,所以
=
,两边平方整理得:x2=4y,
所以曲线C的方程为x2=4y. …(5分)
(2)①证明:因为A(x0,y0)是曲线C:x2=4y上的点,所以y0=
,∴A(x0,
).
又点P、Q在曲线C:x2=4y上,所以可设P(x1,
),Q(x2,
),…(6分)
而直线AP,AQ的倾斜角互补,所以它们的斜率互为相反数,
即
=-
,整理得x1+x2=-2x0. …(8分)
所以直线PQ的斜率kPQ=
=
=-
为定值. …(10分)
②解:由①可知,kPQ=-
,则若点B在曲线段L上,且点B到直线PQ的距离最大,
∴曲线C在点B处的切线l∥PQ. …(11分)
设l:y=-
x+b,代入抛物线方程,消去y,得x2+2x0x-4b=0.
令△=(2x0)2-4×1×(-4b)=0,整理得b=-
.…(12分)
代入方程组,解得x=-x0,y=
.
所以,点B的坐标是(-x0,
). …(14分)
所以M(
| x |
| 2 |
| y+1 |
| 2 |
且圆M的直径为|FF′|=
| x2+(y-1)2 |
由题意,动圆M与x轴相切,所以
| |y+1| |
| 2 |
| ||
| 2 |
所以曲线C的方程为x2=4y. …(5分)
(2)①证明:因为A(x0,y0)是曲线C:x2=4y上的点,所以y0=
| x02 |
| 4 |
| x02 |
| 4 |
又点P、Q在曲线C:x2=4y上,所以可设P(x1,
| x12 |
| 4 |
| x22 |
| 4 |
而直线AP,AQ的倾斜角互补,所以它们的斜率互为相反数,
即
| ||||
| x1-x0 |
| ||||
| x2-x0 |
所以直线PQ的斜率kPQ=
| ||||
| x2-x1 |
| x1+x2 |
| 4 |
| x0 |
| 2 |
②解:由①可知,kPQ=-
| x0 |
| 2 |
∴曲线C在点B处的切线l∥PQ. …(11分)
设l:y=-
| x0 |
| 2 |
令△=(2x0)2-4×1×(-4b)=0,整理得b=-
| x02 |
| 4 |
代入方程组,解得x=-x0,y=
| x02 |
| 4 |
所以,点B的坐标是(-x0,
| x02 |
| 4 |
点评:本题考查轨迹方程的求解,考查直线的斜率,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
